こんにちは。ヤフーのデータサイエンティストの山本です。
ヤフーではさまざまなサービスで「あなたにおすすめ」というようなレコメンデーション・モジュールを提供しています。本記事はそのレコメンデーションにおいて候補アイテムの多様性が高く推薦の難易度が高い二次流通ECのヤフオク!についてご紹介します。
レコメンデーション・システム、二次流通EC、多腕バンディット問題、協調フィルタリング、機械学習リランキングといったキーワードに興味がある方はぜひご覧ください。
この記事で取り扱っているデータは、プライバシーポリシーの範囲内で取得したデータを個人が特定できない状態に加工しています。
2段階モデル・レコメンデーション
ヤフーのように日本全国に多くのユーザーがいるプラットフォームのレコメンデーション・システムは、数千万規模のユーザーかつ数千万規模のアイテムをあつかい、各ユーザーが最も興味のある10〜50件ほどのアイテムを抽出して推薦しています。
膨大なユーザーからのリクエストごとに、膨大なアイテムから高度にパーソナライズされた推薦を行うことは困難です。また、最終推薦アイテムを抽出するうえで、あるユーザーにまったく関係がないユーザーとアイテムの関係性を考慮することは不要な作業です。
例えば、ゴルフには興味があるが、手芸には興味がない人がいたとします。大規模データを用いたレコメンデーション・システムを構築する際、集められた情報は一つのデータとして扱われ、ゴルフ好きユーザーへの行動と手芸好きのユーザーの行動は同時に学習されてしまいます。
これらの背景を踏まえ、私たちのレコメンデーション・システムでは、2段階モデルを採用しています。以下、図のとおり1段目に”協調フィルタリング”、2段目に”リランキング”という構成です。
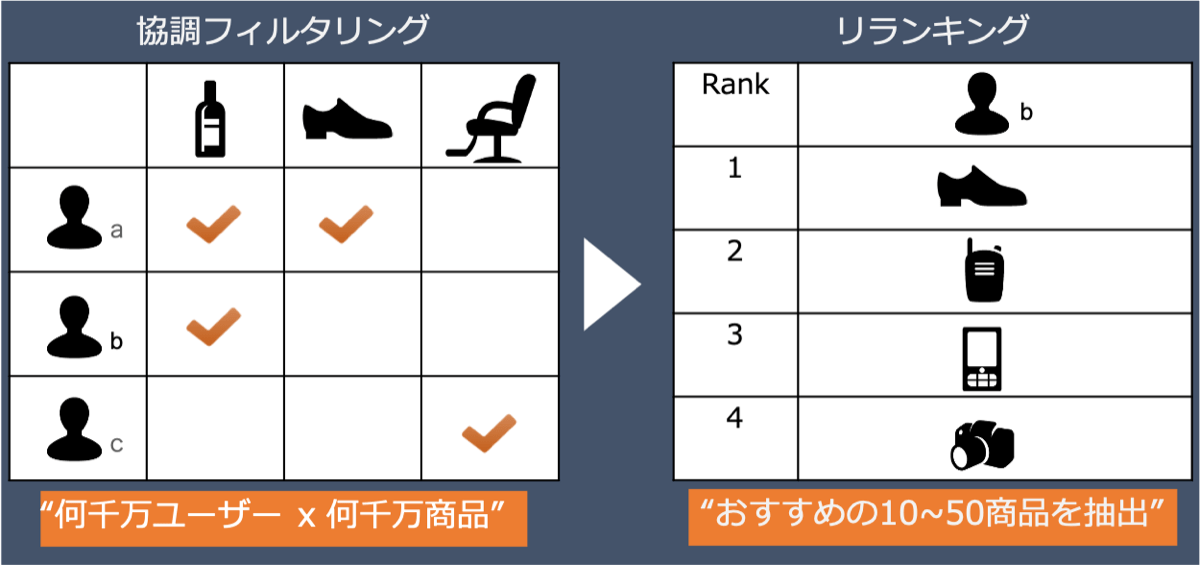
協調フィルタリング
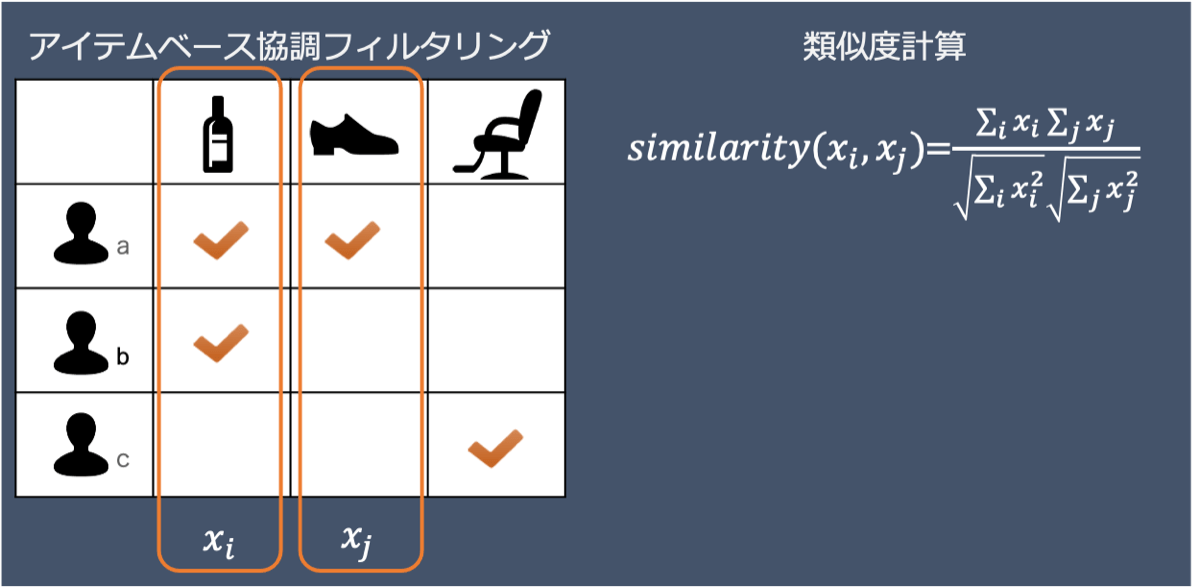
協調フィルタリングはユーザーとアイテムの共起性にもとづいて推薦アイテムの抽出を行います。その中でも私たちはアイテム・ベース協調フィルタリングを1段目のアルゴリズムに利用しています。
主に、それぞれのユーザーのそれぞれのアイテムの閲覧を好意的なフィードバックとして集計します。そこから、あるアイテムを見たユーザーを2値で表現したベクトル(以降、ユーザー・ベクトルと表記)と、別のアイテムのユーザー・ベクトルとの類似度を算出します。最後に、あるアイテムと類似度の高いアイテムの上位100〜200件ほどを1段目の推薦候補アイテムとします。私たちが、1段目にアイテム・ベース協調フィルタリングを利用している利点は以下のとおりです。
- 分散処理環境下でのスケールが比較的に容易
- 類似度計算をあつかうモデルは学習時間が高速
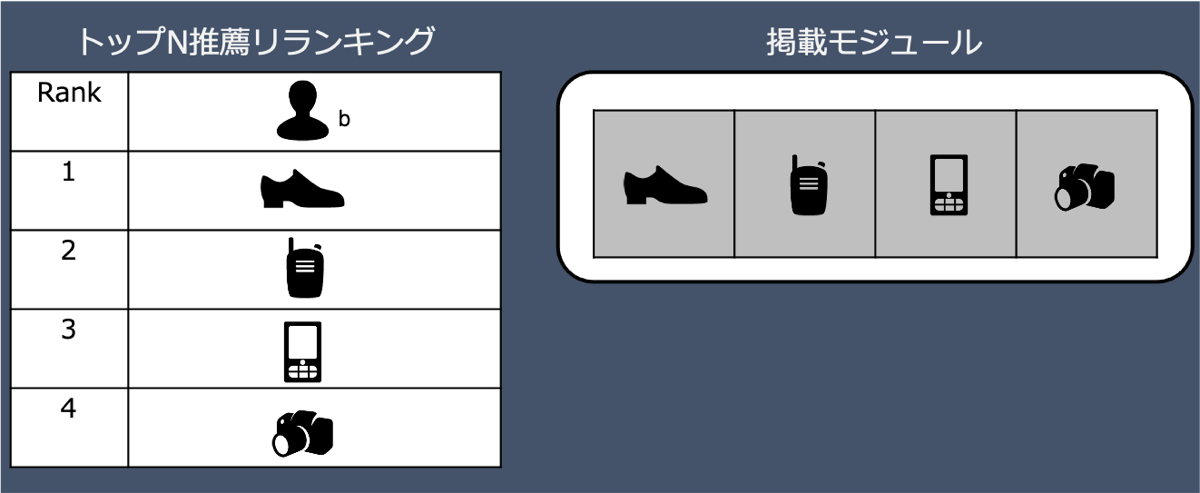
リランキング
1段目の協調フィルタリングにより抽出された100〜200件ほどの推薦候補アイテムを、掲載モジュールに合わせて上位N件(主に10〜20件)に絞り込みます。この処理はトップN推薦リランキングとも呼ばれます。ユーザーにとってより関心の高いアイテムを機械学習モデルなどで選定します。ここで利用する機械学習モデルは、ユーザーとアイテムの属性およびユーザーとアイテムの相互作用を特徴量に使い目的関数に最適化されたものです。私たちが、2段目にトップN推薦リランキングを利用している利点は以下のとおりです。
- ユーザーの関心が高い、かつ掲載モジュールにおさまる推薦アイテムの選定が可能
- 候補アイテムが限られているため、複雑な機械学習モデルを利用しても実時間で計算が可能
通常のECと二次流通ECの違い
この記事を読まれているみなさんは普段どのようなECをお使いですか? ヤフーにはYahoo!ショッピングやPayPayモールなどがありますが、これらのECがあつかう商品は主に新品です。一方、ヤフオク!のような二次流通ECは個人の売り手による中古品もしくは買ったけど未開封の新品などが売られています。古物商業者のように個人ではない方もいらっしゃいますが、あつかう商品は同じです。この通常のECと二次流通ECの違いをまとめてみました。
| 通常のEC |
|---|
| 流通商品は主に製造元が販売中のものが多い |
| 小売店舗も多くの在庫を保持している |
| 新品のため商品の状態に差がない |
| 二次流通EC |
|---|
| 流通商品は製造が終了もしくは生産が少ないものが多い |
| 個人・古物商業者に限らず保有商品の在庫は1点ものが多い |
| 商品の状態は千差万別 |
レコメンデーション・システムはAmazonなど通常のECから発展した経緯がありますが、この二次流通ECの特性をうまく扱うためには考慮するべきことがあります。その考慮すべきことと、解決方法を以降でご紹介します。
「落札できる」それが問題
あらためて、ヤフオク!などオークションにおける入札の仕組みについて説明します。ここでお話しする内容はオークションに限らずフリマなど二次流通EC全般に言える課題です。
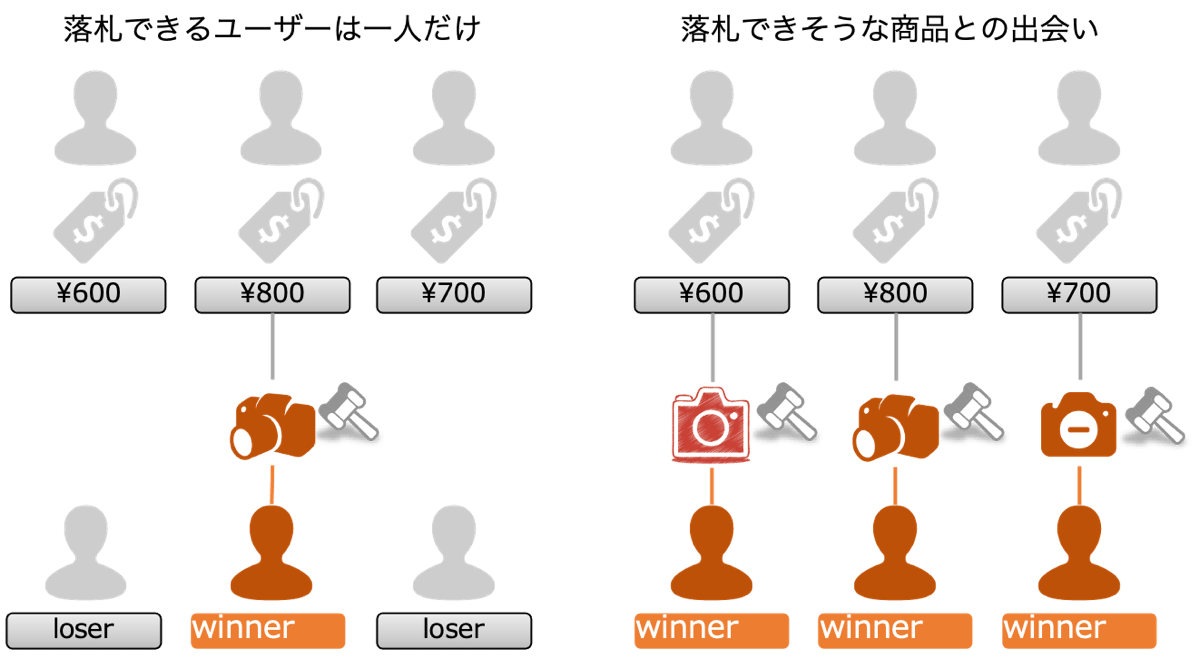
以下左図のように、ある3名のユーザーが一眼レフカメラを購入したいとします。しかし、ユーザーの希望に沿う商品はたった一つしかない、もしくは一つしか認知されていない、とします。この場合、オークションでは最も高い価格を入札したユーザーが購入者となり、他のユーザーは購入したかったけど購入できなかった非購入者になります。ものが溢れる時代でありながら、需要が満たされないことが頻発するのが二次流通ECの特徴です。解決方法は、右図のようにユーザーが希望する価格・状態および品質を確保しながら落札できそう(購入できそう)な商品とユーザーを出会わせることです。
このように、二次流通ECのレコメンデーション・システムは「落札できる」商品を推薦する必要があります。
多腕バンディット問題
多腕バンディット問題は、複数の選択肢に対して、そのいずれかを選んだときにしかそれぞれの選択肢に関する情報を得られない状況で、最終的な利得を最大化する問題設定です。
例えば、当たりが出る確率が分からない3台のスロットマシーンをランダムに10回プレイしたとします(以下左図)。その際に判明したスロットマシーンの勝率は、A:50%(1/2)B:33%(1/3) C:40%(2/5)だったとします。この時点でスロットマシーンAが最も良いと分かったので、それ以降、Aのみでプレイするという選択も可能です。とはいえ、たかだか10回のプレイでは真の勝率が分からないので、さらにランダムでプレイし続けるという選択も考えられます。ここであげた2つの選択もしくは意思決定は、多腕バンディット問題において前者を「活用」、後者を「探索」と言います。「活用」は、その時点で知り得た最良の選択をすることで、「探索」は、新しい情報を得るための選択をすることです。
仮に、ランダムに3,000回プレイしたときに真の勝率が得られたとして結果が、A:12% B48% C:24%だったとします(以下右図)。ようするに、真に勝率の高いスロットマシーンがBだった場合です。ここで、1回の勝利で得られる報酬を1円として、最初からBを3,000回プレイした場合と、ランダムに3,000回プレイした場合で得られる合計金額の差額を計算すると、600円です。この600円は、本当に得られたはずの報酬から失った報酬です。これを多腕バンディット問題では「リグレット」と呼びます。この「リグレット」を最小化するために「活用」「探索」を調整する仕組みを「方策」と言い、数学的に定式化されたものが多腕バンディット・アルゴリズムです。

フリーケンシーキャップUCB
ここまででお伝えした二次流通ECの課題をレコメンデーション・システムと多腕バンディット・アルゴリズムで解決します。
- ユーザーの課題
- 商品の価格・状態や品質が希望に沿う、なおかつ入札で勝ち抜いて落札できそうな商品を知りたい
- レコメンデーション・システムの提案
- ユーザーが未知の商品を探索的に推薦して、落札できそうかをユーザーに評価してもらう
この解決を具体的に示した多腕バンディット・アルゴリズムが私たちが考案した以下のフリーケンシーキャップUCBです。
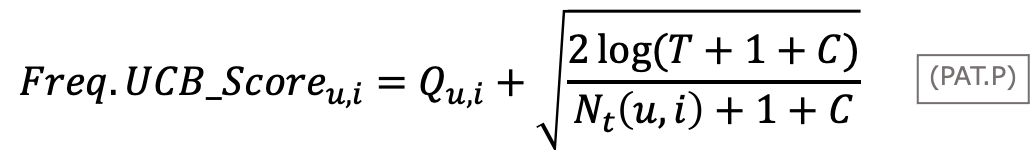
フリーケンシーキャップUCBは、2段階モデル・レコメンデーションのリランキング・モデルと組み合わせて定式化しています。ここで、全体のユーザー![]() に対して推薦を行うユーザーを
に対して推薦を行うユーザーを![]() 、全体のアイテム
、全体のアイテム![]() に対して推薦を行うアイテムは
に対して推薦を行うアイテムは![]() 、時系列
、時系列![]() におけるある時刻
におけるある時刻![]() とした場合、
とした場合、
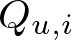 : 2ndモデルによるユーザー
: 2ndモデルによるユーザー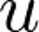 に対するアイテム
に対するアイテム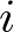 のリランキングスコア
のリランキングスコア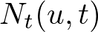 : ある時刻
: ある時刻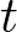 におけるユーザー
におけるユーザー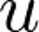 にアイテム
にアイテム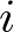 を推薦した回数
を推薦した回数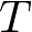 : あるユーザー
: あるユーザー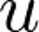 に推薦を行った回数
に推薦を行った回数 : 初期推薦回数です。
: 初期推薦回数です。
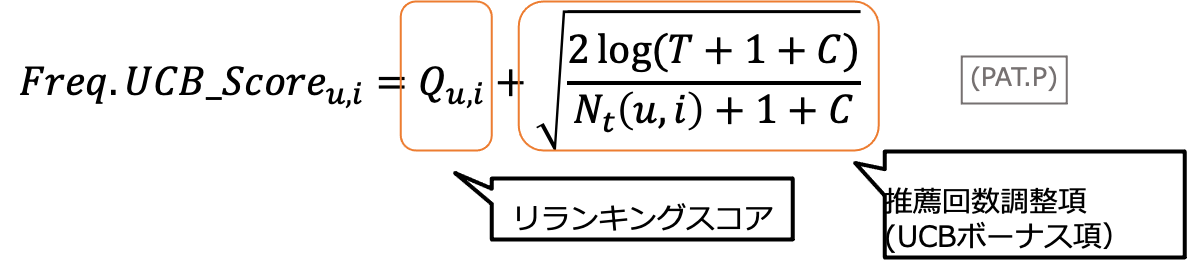
この式では、右辺第一項の「リランキングスコア」に第二項の「推薦回数調整項」が加えられています。「推薦回数調整項」はあるアイテムがユーザーに推薦された回数が少ないほど高くなり、推薦回数が多いほど小さくなります。ようするに、ユーザーにとって目新しいアイテムほど探索的に推薦され、推薦回数がある程度の数に到達するとリランキングスコアのみが用いられます。
参考までに、フリーケンシーキャップUCBの原型であるUCB1は以下の通りです。アーム選択回数が考慮されていることと推薦回数が考慮されていることの対応付けは同じです。一方、報酬関数はリランキングスコア、方策の決定はアーム選択ではなく推薦アイテムの期待値となっている点が異なります。
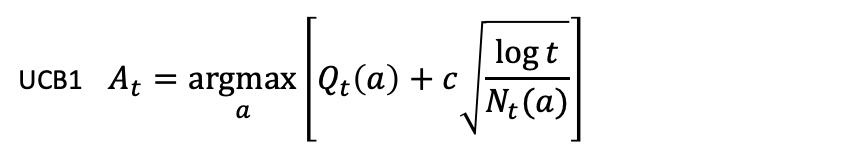
フリーケンシーキャップUCBのデモ
では、実際のレコメンデーション・システムでフリーケンシーキャップUCBを動かしてみます。想定するユースケースは以下の通りです。
| 項目 | 値 |
|---|---|
| レコメンデーション・モジュール | ユーザー訪問ごとに6件のアイテムを表示 |
| 推薦候補アイテム | 20件 |
| リランクスコア(推薦優先順位) | 1.0 ~ 0.0 |
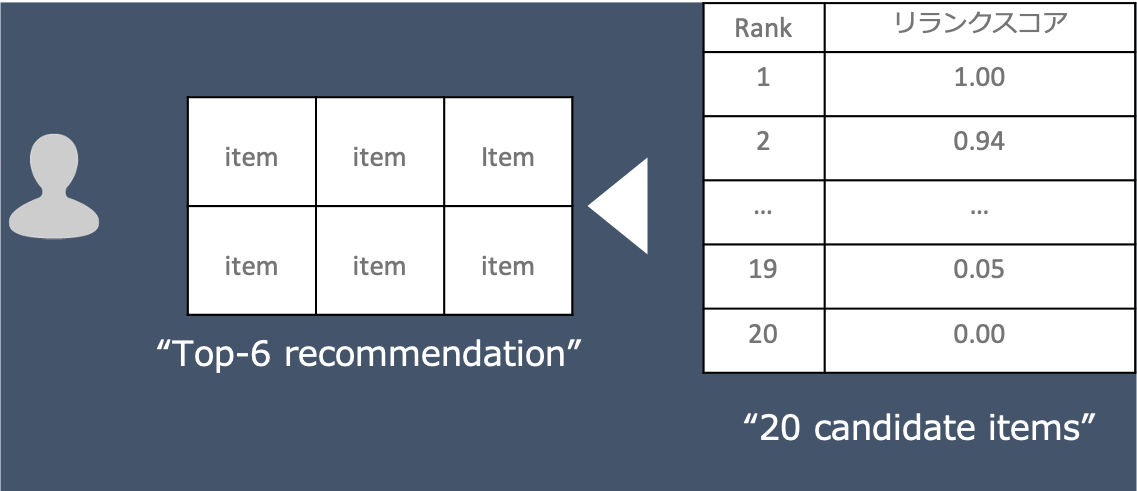
1.ユーザー初回訪問 (![]() =0,
=0, ![]() =1)
=1)
ユーザーの初回訪問時はリランクスコアがそのまま利用されるため、図右側の推薦候補アイテム上位6件がレコメンデーション・モジュールに表示されます。
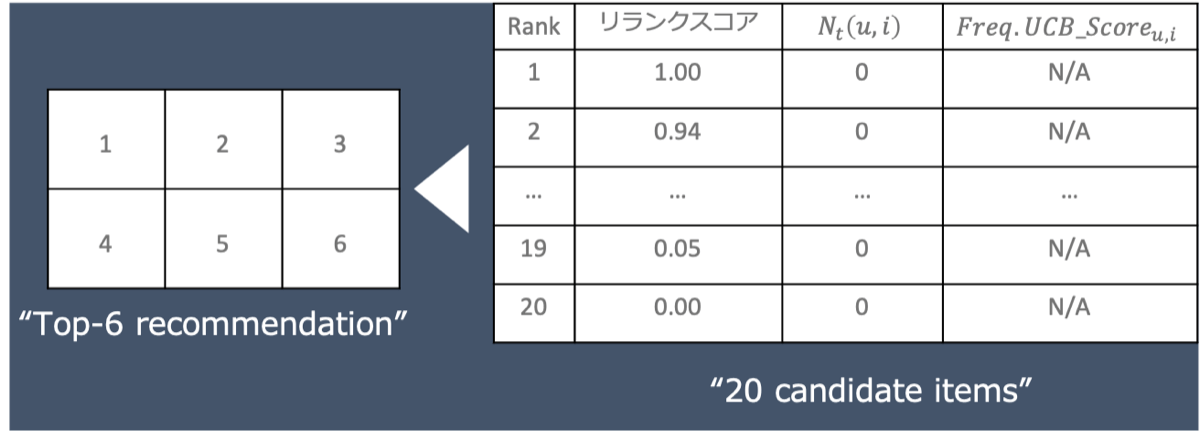
2.ユーザー訪問2回目 (![]() =1,
=1, ![]() =1)
=1)
初回訪問により![]() と
と![]() がそれぞれカウントされました。この値を利用してフリーケンシーキャップUCBスコアを算出します。今度は、フリーケンシーキャップUCBスコアが高い順に推薦候補アイテムを決定します。その結果、もとは上位6件に含まれなかった順位7, 8のアイテムがレコメンデーション・モジュールに表示されます。これは、探索的にアイテムが推薦されている状況を示しています。
がそれぞれカウントされました。この値を利用してフリーケンシーキャップUCBスコアを算出します。今度は、フリーケンシーキャップUCBスコアが高い順に推薦候補アイテムを決定します。その結果、もとは上位6件に含まれなかった順位7, 8のアイテムがレコメンデーション・モジュールに表示されます。これは、探索的にアイテムが推薦されている状況を示しています。
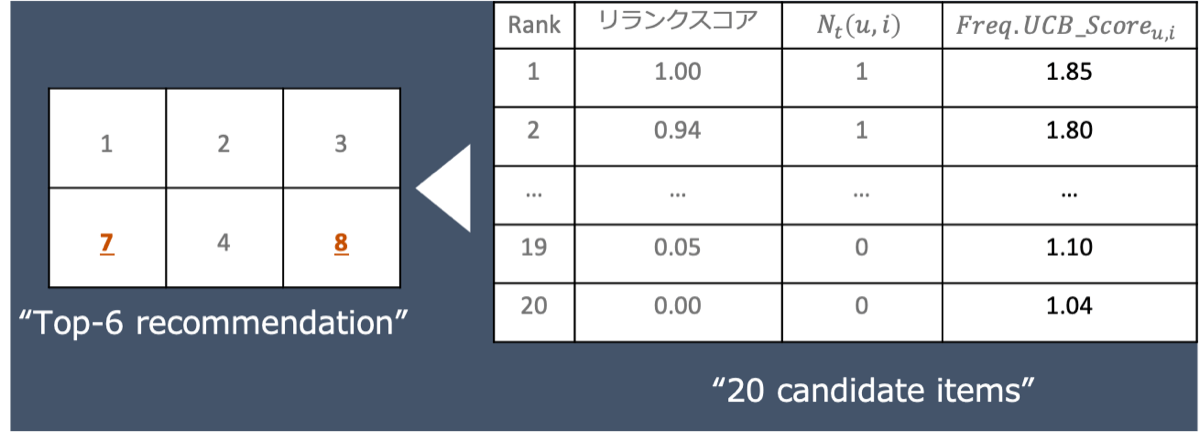
3.ユーザー訪問3回目 (![]() =2,
=2, ![]() =1)
=1)
次は3回目の訪問です。あるユーザーへの推薦回数![]() は2回目と同じようにカウントされますが、
は2回目と同じようにカウントされますが、![]() については重み付けがそれぞれの推薦候補アイテムでバラツキが生じ始めます。この影響により、順位9のアイテムがレコメンデーション・モジュールに表示されます。また、順位5, 6のアイテムのようにユーザー訪問2回目で推薦から除外されたアイテムも再度表示に戻ってきています。
については重み付けがそれぞれの推薦候補アイテムでバラツキが生じ始めます。この影響により、順位9のアイテムがレコメンデーション・モジュールに表示されます。また、順位5, 6のアイテムのようにユーザー訪問2回目で推薦から除外されたアイテムも再度表示に戻ってきています。
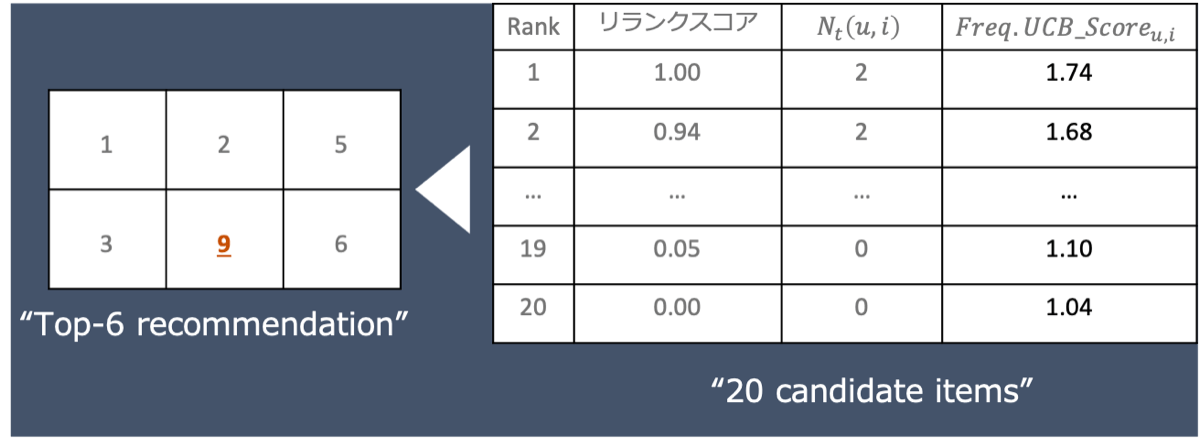
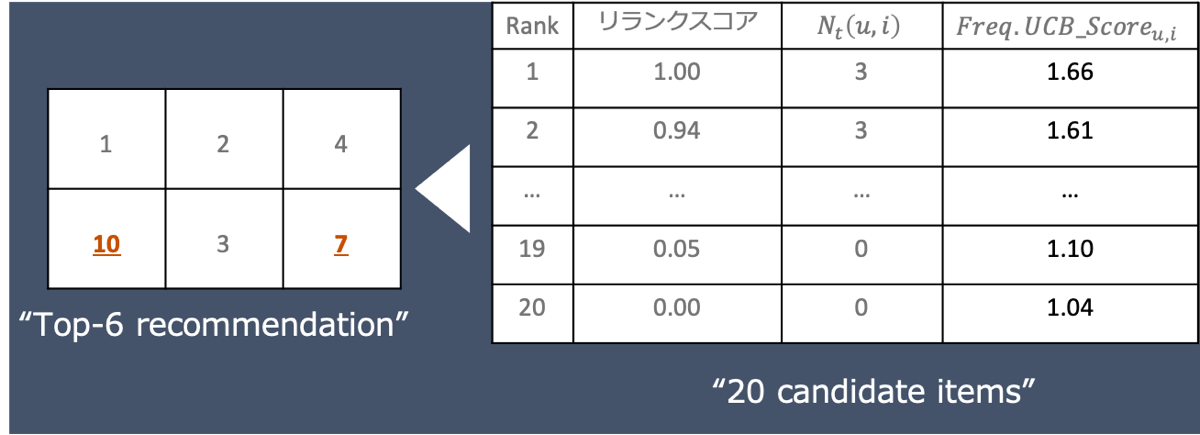
4.ユーザー訪問4回目 (![]() =3,
=3, ![]() =1)
=1)
最後の4回目の訪問です。カウントやフリーケンシーキャップUCBスコアの算出は2回目、3回目と同じです。この4回目の訪問では、順位10のアイテムが初めて表示されています。このように、下位のアイテムであってもユーザーにとっては未知のアイテムであれば、探索的に推薦されます。
おわりに
本記事では、大規模かつ多種多様なアイテムを扱う二次流通ECのレコメンデーション・システムにおいて、いかにユーザーが落札できそう・購入できそうと思えるアイテムを引き合わせる仕組みを紹介しました。そのなかで、一般的なレコメンデーション・システムでは解決が難しいユーザーが未知のアイテムへの評価、ユーザーがそのアイテムにどのような反応を示すのか、それを知るために多腕バンディット・アルゴリズムを利用したフリーケンシーキャップUCBという独自のアルゴリズムも紹介しました。
これらの技術が、皆さんが直面しているレコメンデーション・システムの課題の解決方法となれば幸いです。
関連リンク
こちらの記事のご感想を聞かせください。
- 学びがある
- わかりやすい
- 新しい視点
ご感想ありがとうございました




