高次元ベクトルデータの近傍検索エンジンNGT(OSS)の研究開発を行っているYahoo! JAPAN研究所の岩崎です。NGTを利用した類似画像検索や物体認識にも関わっています。グラフ構造型の性能ボトルネックを改善できる手法として、2021年1月にNGTのインデックスとして追加したQG(Quantized graph)を解説します。
他にも10億ものベクトルを検索できるQBG(Quantized blob graph)を2022年8月にリリースしているのですが、これは別の機会に解説します。
グラフ構造型インデックスの限界?
ベクトル近傍検索には主にツリーやグラフ構造の手法と量子化による手法があります。NGTはグラフ構造型インデックス(詳細は「NGT -グラフ型インデックスによる近似近傍検索の基本-」をご参照ください)を用いており、グラフの構造がその性能に大きく影響します。Yahoo! JAPAN研究所は独自のONNG[1]というグラフを提案し、世界トップクラスの性能を達成しました。しかし、グラフ構造の改良は限界に近づいているとも言えます。とは言え、探索効率(検索結果の距離計算を行ったベクトル数に対する実際に検索結果となったベクトル数の割合)は量子化系手法の探索効率より良い傾向があります。
では、何がボトルネックになっているかというとメモリからベクトルをフェッチしてくる時間です。これに対処するためにプリフェッチ(詳細は「NGT - 検索ロジックの詳細と実装方法 -」をご参照ください)を行っていますが、これにも限界があります。そこで、フェッチ時間を減らすためにベクトルのサイズ自体を小さくしてしまう方法が考えられます。QGではベクトルの圧縮のために直積量子化(product quantization)[2]を採用しています。
通常の直積量子化は転置インデックス(inverted index)と組み合わせますが、QGではグラフと組み合わせている点が独自の構造になっています。つまり、グラフの探索は今まで通りで、距離計算部分だけに直積量子化を導入しています。では、次にベクトル量子化、直接量子化を簡単に説明します。
ベクトル量子化
左下図のように2次元ベクトル(黒点)があったとします。この空間を一定間隔で分割し、それぞれの領域の中心のベクトル(青点)でその領域内のベクトルを表現できます。この場合、4つの領域なので0から3の数字ですべてのベクトルを表現できます。つまり、2ビットで表現できます。これをベクトル量子化と呼びます。
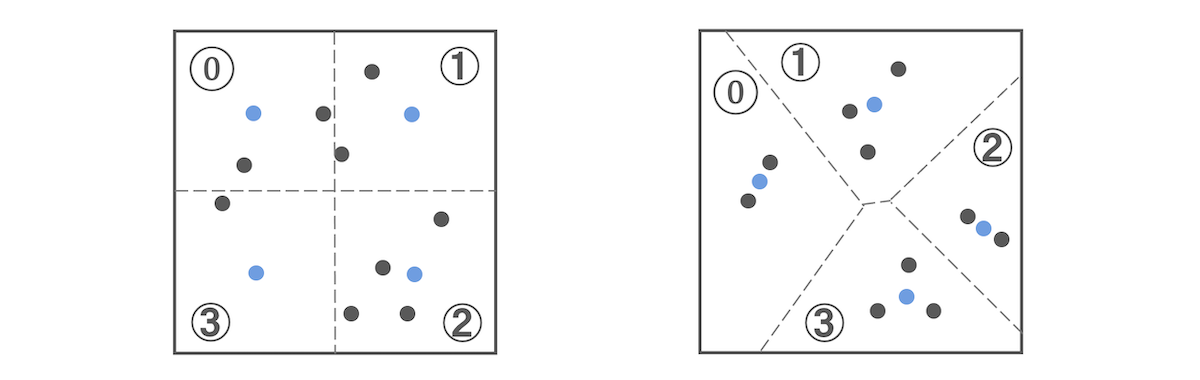
なお、中心ベクトルと元ベクトルの差分(距離)が誤差(量子化誤差)となります。通常、ベクトル量子化では、この誤差をなるべく減らすために、すべてのベクトルをクラスタリング(k-means)して空間をクラスタに分割します。クラスタリングした結果が右上図です。各ベクトルが中心ベクトル(青点)の近くに位置していることが分かります。このベクトル量子化でもクラスタ数を増やせば誤差を減らすことはできますが、一方で、中心ベクトルを表現する最大値(この図では3)の桁数が大きくなるのでデータサイズが増加します。つまり、数万といったクラスタに分割するとそれを表現するのに少なくとも2バイト必要です。そこで、誤差を抑制しつつ、データサイズの増加も抑制する方法が次に説明する直積量子化です。
直積量子化
元ベクトルを複数の部分ベクトルに分割した上で、それぞれの部分ベクトルにベクトル量子化を行うのが直積量子化です。下図は8次元のベクトルを4つの部分ベクトルに分割した直積量子化の例です。この例では量子化のクラスタは4つなので、各部分ベクトルは0から3の値で表現できます。下図の例では、元ベクトルは1次元当たり浮動小数点4バイトなので8次元のベクトルで32バイトです。これが直積量子化により1次元当たり2ビットなので4次元のベクトルで1バイトの量子化ベクトルに圧縮できます。つまり、1/32に圧縮できたことになります。また、部分ベクトル単位に量子化することにより量子化誤差も少なくなります。量子化のクラスタ数は数百や数千という場合もありますが、QGでは高速化のために16としています。これについては後述します。
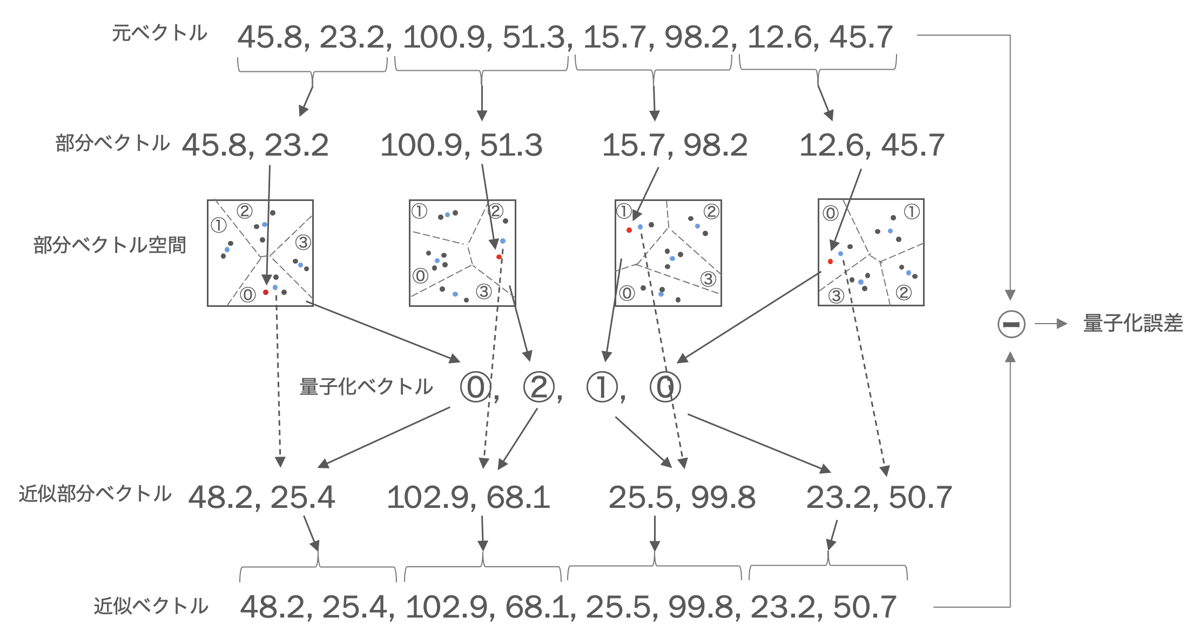
なお、量子化ベクトルから元のベクトルは復元できませんが、上図のように中心ベクトルからなる近似ベクトルを生成できます。近似ベクトルと元ベクトルの差分が量子化誤差となり、検索時の精度に影響してきます。
直積量子化における近似距離計算の高速化
直積量子化によりベクトルを大幅に圧縮できるのでメモリからの量子化ベクトルのフェッチの高速化ができます。その一方で量子化ベクトルから近似ベクトルを生成する手順が増えるので距離計算コストが増加してしまいます。そこで、直積量子化では、ベクトル単位に近似ベクトルを生成し近似距離を計算するのではなく、個々の部分ベクトル単位に距離を計算した上で、複数のベクトルの近似距離を一括して計算することで総距離計算時間を削減しています。図のように、まず、検索開始時に、指定されたクエリベクトルと、各部分ベクトル空間における各クラスタの中心ベクトルとの距離(正確には距離の二乗)をすべて算出し、ルックアップテーブルを作成します。
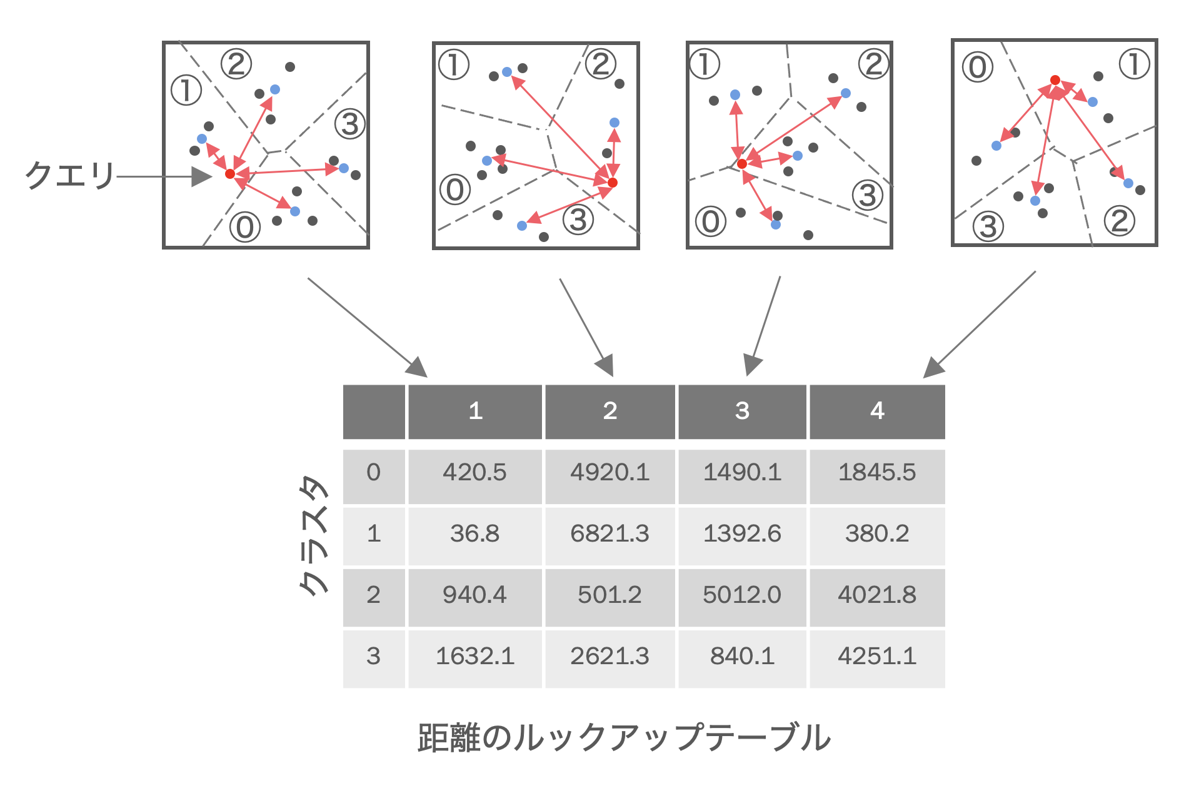
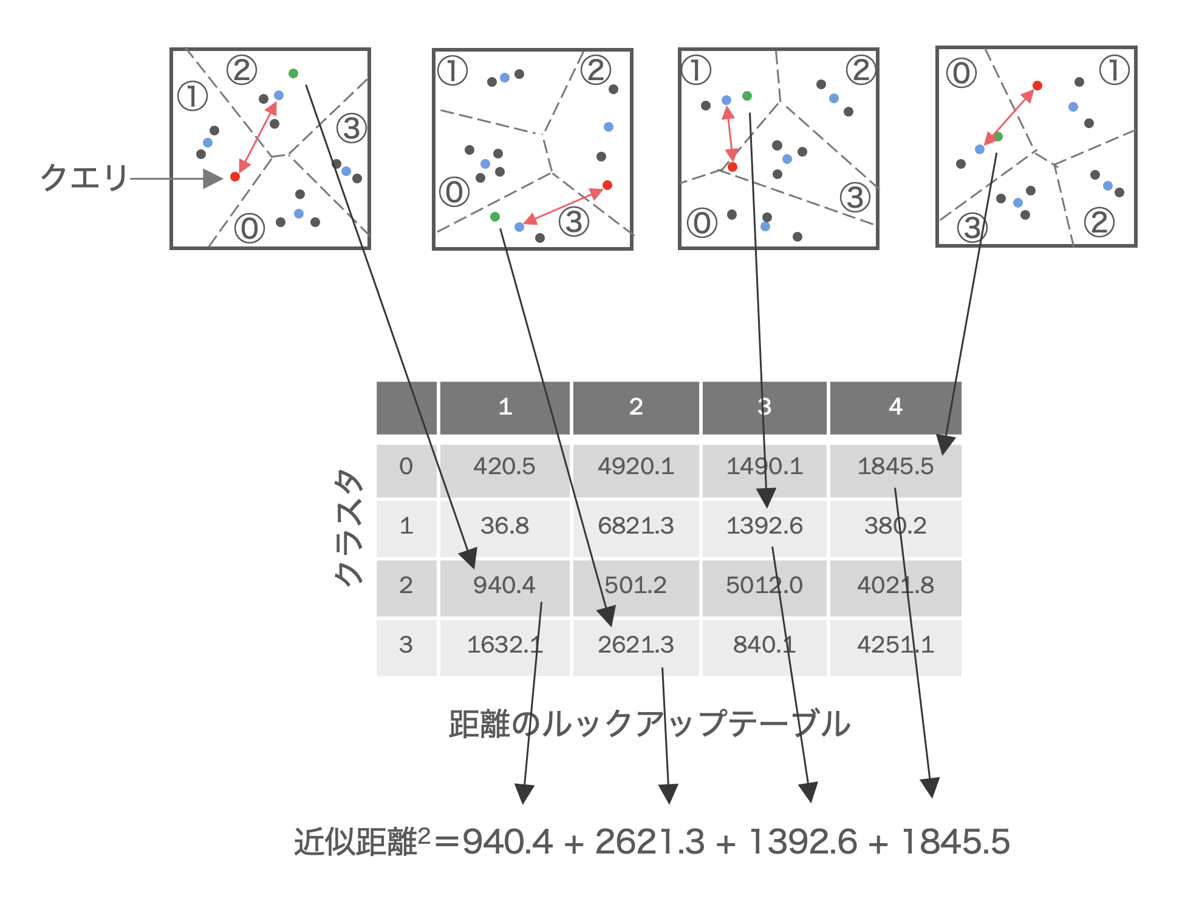
各ベクトルとクエリとの近似距離はこのルックアップテーブルの各部分空間の距離の合計により計算できます。つまり、図の緑をクエリとの近似距離を算出したいベクトルだとすると、そのベクトルが属する部分空間の距離をルックアップテーブルから取得し加算するだけで近似距離が算出できます。テーブル上の距離の加算だけで近似距離を算出できるので、この空間内にベクトルが多数あればあるほど、個々のベクトルごとに距離計算するよりも総計算時間が短縮されます。
グラフ探索と直積量子化の融合
上記のように直積量子化により近似距離を高速に算出できます。ただ、高速だといっても数百万ものベクトルの近似距離を算出するにはかなりの時間がかかってしまいます。そこで、クエリに対して近傍であろう候補ベクトルに絞り込んだ上でそのベクトル集合に対して近似距離の計算を行います。通常、事前に全ベクトルをクラスタリングして多数に分けたクラスタ単位で絞り込みます。つまり、検索時にクエリに対して近傍のクラスタを選択し、そのクラスタ内のベクトルに対して近似距離計算を行います。
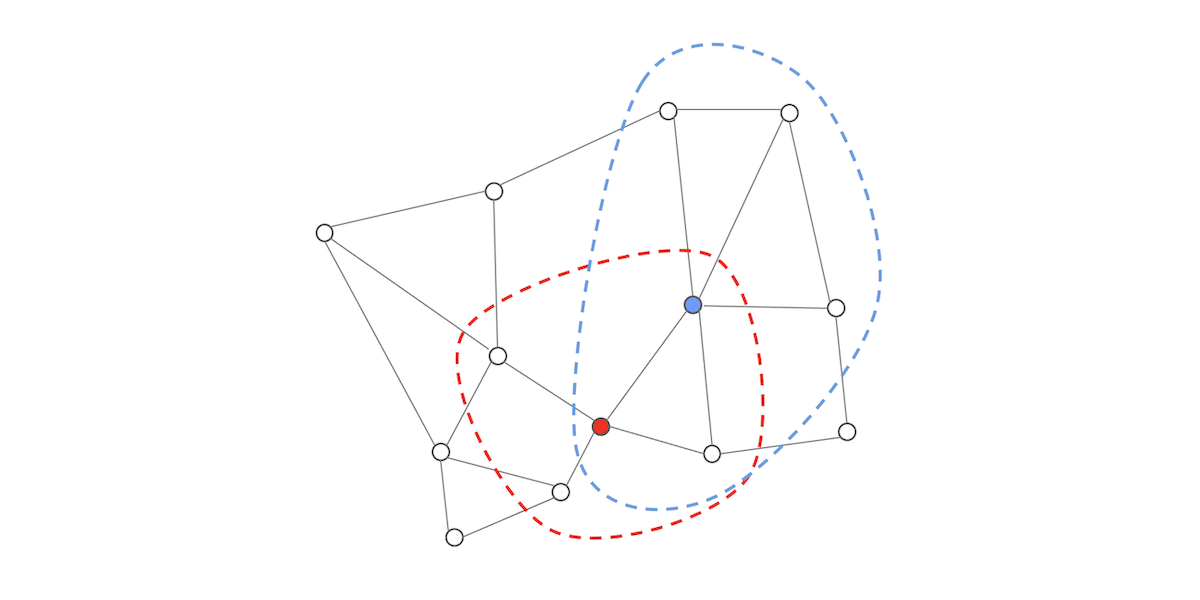
NGTでは近傍のベクトル間が接続されており、グラフを構成しています。そのグラフを探索してクエリに対する近傍ベクトルを検索(詳細は 「NGT -グラフ型インデックスによる近似近傍検索の基本-」をご参照ください)します。グラフ探索中に、対象ベクトルに接続されている複数のベクトルの中で、いずれのベクトルが最もクエリに近いかを知る必要があります。つまり、その複数のベクトルとクエリ間との距離が必要です。この距離計算に直積量子化の近似距離計算を利用しています。例えば下図のようなグラフで、赤のベクトルが探索対象の場合には赤点線内のベクトルに対して一括して直積量子化による近似距離計算を行います。同じように青のベクトルが探索対象の場合には青点線内のベクトルに対して一括して近似距離計算を行います。この図の場合には接続されているベクトル数が少ないですが、実際には各ベクトルは10以上もの近傍のベクトルに接続しています。
なお、直積量子化による検索をよくご存じの方のために補足すると、直積量子化による検索では、全ベクトルから絞り込んだクラスタの中心ベクトルと各ベクトルの残差ベクトルを用いて直積量子化を行いますが、QGでは高速化を優先して、残差ベクトルを用いていません。
近似距離計算の高速化
前述の通り、ルックアップテーブルを使うことで高速化されるのですが、ルックアップテーブルから個々の距離をフェッチする時間がボトルネックです。そこでルックアップテーブルの距離の表現を1バイトに圧縮することでルックアップテーブルを小さくしてフェッチ時間を短縮し、かつ、SIMD命令を用いることで近似距離計算を高速化する手法[3]を採用しています。SIMD命令で高速に参照できるルックアップテーブルの最大要素数が16なので直積量子化のクラスタ数を16としています。
性能測定結果
ANN-Benchmarks[4]でQGの性能測定(時間制限は5時間)を行いました。以下に、NGTのPANNG[5]、ONNG、QGおよび主な手法(ScaNN、HNSW、Annoy)について、いくつかのデータセットを用いた結果を紹介します。横軸が再現率、縦軸が1秒間当たりの処理クエリ数です。グラフ上で右上に位置するほど性能が高いことを意味します。 グラフ中のNGT-qgが今回解説したQGです。QGがすべてのデータセットでトップというわけではありませんが、高い性能を示しています。

使用方法
NGTのインストールの方法はこちらをご覧ください。QGはNGTのグラフ構造型インデックスでの距離計算部分に直積量子化を導入しただけなので、まず、今まで通りグラフ型インデックスを生成します。その後に、直積量子化のインデックスを生成します。
サンプルデータ(1,000,000ベクトル)の準備です。
$ curl -L -O https://github.com/yahoojapan/NGT/raw/main/tests/datasets/ann-benchmarks/sift-128-euclidean.tsv
$ curl -L -O https://github.com/yahoojapan/NGT/raw/main/tests/datasets/ann-benchmarks/sift-128-euclidean_query.tsv
$ head -1 sift-128-euclidean_query.tsv > query.tsv次に、以下のようにグラフ構造型インデックス(ANNG)を生成します。この例では、次元数128、ユークリッド距離を指定しています。さらに ANNGからONNGを生成すれば、性能が向上しますが、ここでは、ONNGの生成は省略します。
$ ngt create -d 128 -D 2 anng sift-128-euclidean.tsvもちろん、この状態でグラフを使って検索できます。
$ ngt search anng query.tsv
Query No.1
Rank ID Distance
1 932086 232.871
2 934877 234.715
3 561814 243.99
...
20 236648 275.144
Query Time= 0.00623724 (sec), 6.23724 (msec)
Average Query Time= 0.00623724 (sec), 6.23724 (msec), (0.00623724/1)この後、QGの初期化を行います。ディレクトリanngの中に空のQGのインデックスが生成されます。
$ qbg create-qg anngQGのインデックスを生成します。
$ qbg build-qg anngこれで、QGを使って検索できます。この例ではグラフを使った検索結果と同じになるようにepsilonを指定しています。
$ qbg search-qg -e 0.06 anng query.tsv
Query No.1
Rank ID Distance
1 932086 232.871
2 934877 234.715
3 561814 243.99
...
20 236648 275.144
Query Time= 0.00150579 (sec), 1.50579 (msec)
Average Query Time= 0.00150579 (sec), 1.50579 (msec), (0.00150579/1)おわりに
以上、QGの仕組みと使用方法でした。次回はQBGを解説する予定です。
なお、NGTの研究開発をお手伝いしていただける方を募集しています。ご興味ある方はこちらにご連絡ください。
Yahoo! JAPAN研究所 岩崎雅二郎
NGT関連リンク
応用事例
- 写真から施設名や観光名所を識別する、画像認識モデルとシステム紹介
- Yahoo! JAPAN、特許庁主催の「AI×商標 イメージサーチコンペティション」で第1位を獲得
- スマホで撮った写真からも検索可能に!類似画像検索アプリの3つの新機能とシステム紹介
- ヤフーの類似画像検索技術と特徴量モデル
- Yahoo!ショッピングの類似画像検索 〜 近傍探索NGTの導入事例
- 大規模特定物体認識のショッピングサービスへの適用 〜サイヤスカメラの紹介〜
NGTの解説
- NGT -グラフ型インデックスによる近似近傍検索の基本-
- NGT - グラフの探索起点の選択方法 -
- NGT - 検索ロジックの詳細と実装方法 -
- NGT - 最適化グラフの生成方法 -
- 近傍検索のNGTが世界トップレベルの速度達成 〜 ベンチマーク結果とann benchmarksの紹介
- Python版近傍検索NGT(ngtpy)の使い方
参考文献
[1]: Iwasaki, M., & Miyazaki, D. (2018). Optimization of indexing based on k-nearest neighbor graph for proximity search in high-dimensional data. arXiv preprint arXiv:1810.07355.
[2]: Jegou, H., Douze, M., & Schmid, C. (2010). Product quantization for nearest neighbor search. IEEE transactions on pattern analysis and machine intelligence, 33(1), 117-128.
[3]: André, F., Kermarrec, A. M., & Le Scouarnec, N. (2017, June). Accelerated nearest neighbor search with quick adc. In Proceedings of the 2017 ACM on International Conference on Multimedia Retrieval (pp. 159-166).
[4]: Aumüller, M., Bernhardsson, E., & Faithfull, A. (2020). ANN-Benchmarks: A benchmarking tool for approximate nearest neighbor algorithms. Information Systems, 87, 101374.
[5]: Iwasaki, M. (2016). Pruned bi-directed k-nearest neighbor graph for proximity search. In Similarity Search and Applications: 9th International Conference, SISAP 2016, Tokyo, Japan, October 24-26, 2016, Proceedings 9 (pp. 20-33). Springer International Publishing.
こちらの記事のご感想を聞かせください。
- 学びがある
- わかりやすい
- 新しい視点
ご感想ありがとうございました




