こんにちは。Yahoo!広告のデータマーケティングソリューション(以下、DMS)を開発しているデータアナリストの小林です。
私たちのチームは広告効果の分析を目的としたソリューションを数多く提供しています。タッチポイントの複雑化や広告戦略の多様化により、従来の手法では効果分析が困難な時代になったのですが、さまざまな手法によってこの分析精度を向上できています。本記事ではその中のひとつであるアトリビューション分析の仕組みと、ゲーム理論の一手法であるシャープレイ値を適用した発展的な手法についてご紹介します。
シャープレイ値は機械学習モデルの解釈に用いられるSHAP(SHapley Additive exPlanations)というライブラリの基になっている理論として有名ですが、この記事を通してシャープレイ値が広告効果分析の手法として応用できることを知って頂ければ幸いです。
本記事ではDMS全体についての説明は省略しますので、詳細を知りたい方はこちらをご覧ください。
アトリビューション分析とは
アトリビューション分析を簡単に説明すると、「ユーザーがコンバージョン(以下、CV)に至るまでに接触した各広告の貢献度を分析する手法」のことです。
例として、あるユーザーが商品購入に至るまでの次のような経路があるとします。
- ヤフーのトップページで広告Aを見て、とある商品について認知
- その商品に興味を持ち、検索エンジンで検索した際に表示される検索広告Bをクリックして詳細を閲覧
- さまざまな口コミサイトをみつつ最終的に広告Cをクリック
- 商品を購入(CV)
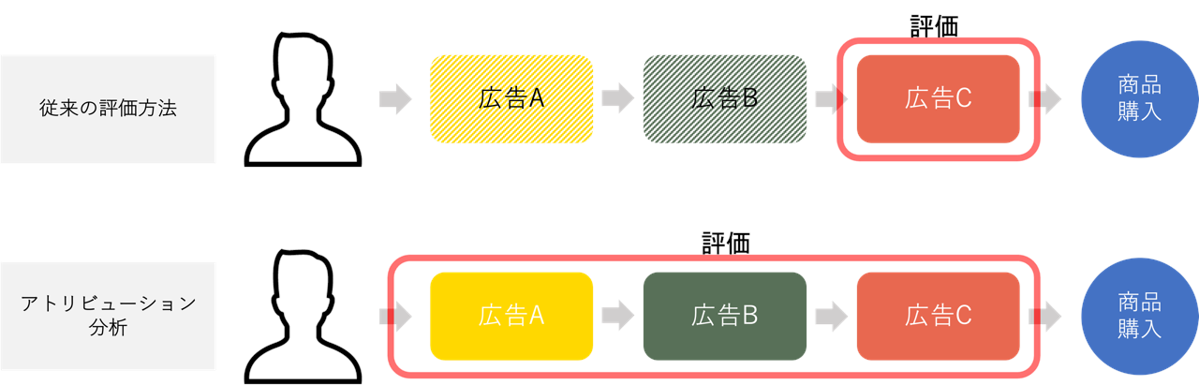
従来は最後のタッチポイントである広告CのみがCVに寄与したと判断し評価されていました。こうした分析ではラストタッチより前のタッチポイントである広告A、Bがユーザーにどのように作用したのかがわからず、アッパー・ミドルファネルを対象とした広告の効果を正しく評価できませんでした。
このような課題に対して、アトリビューション分析ではユーザーがCVに至るまでのタッチポイントを時系列で分析し、その間接的な貢献度を定量的に可視化することで、施策の評価や費用の再分配などのアクションに正しくつなげることができます。
(※分析にあたり、ヤフーではお客様のプライバシーの保護に細心の注意を払っています。詳しくはYahoo! JAPAN プライバシーセンターをご覧ください。)
アトリビューション分析を実施する場合、商材やビジネスモデル、広告目的によって最適な貢献度の配分方法が異なります。そこでまずは、この配分方法を表すアトリビューションモデルのうち代表的な5つを紹介します。
従来のアトリビューションモデル
アトリビューション分析ではCVに至るまでのタッチポイントを基に貢献度を配分します。その配分方法には以下のような5つの代表モデルがあり、それぞれビジネスモデルや広告目的によって使い分けています。
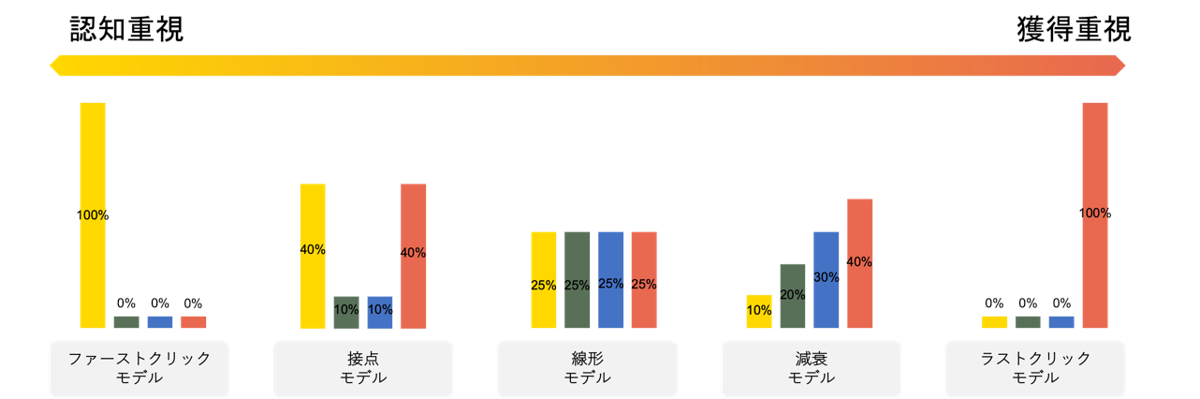
具体的な貢献度の配分方法は以下のとおりです。
| モデル | 貢献度配分方法 |
|---|---|
| ファーストクリックモデル | 最初の接点となった広告にのみCV貢献度を付与 |
| 接点モデル | 最初と最後の接点に対して比重を重く、残りを中間接触へ均等に付与 |
| 線形モデル | 全ての接点に均等にCV貢献度を付与 |
| 減衰モデル | 最後の接点となった広告に最も多く貢献度を割り振り、最初の接触に向かうにつれて線形的に貢献度を減衰させつつ付与 |
| ラストクリックモデル | ラストクリックとなった広告のみにCV貢献度を付与 |
CVまでの経路が長くなってくるとそれぞれのモデルによって算出される貢献度は大きく異なる場合があります。そのため、積極的な認知目的であればファーストクリックモデル、経路の入口と出口をバランス良く評価したい場合は接点モデル、というように目的によって適切なアトリビューションモデルを選択する必要がでてきます。
従来モデルの課題
貢献度配分方法についての代表的なモデルをご紹介しましたが、タッチポイントの複雑化や広告戦略の多様化により、従来のモデルは次のような課題を抱えています。
- いずれのモデルも貢献度の配分割合が恣意的であり、現実に即した結果が得られにくい
- 目的が明確でない場合、最適なモデルの選択や分析結果の解釈が難しい
そこで私たちはこれらの課題を解決すべく、協力ゲーム理論の利得分配法の1つであるシャープレイ値に基づき、CVに至るまでに接触した広告とその過程に応じて、公正に貢献度を分配する手法を採用しました。
今回導入するシャープレイ値とは
協力ゲーム理論では、あるゲームを複数プレーヤーが協力して獲得した報酬を分配するような状況を考えます。
このときプレーヤー間でどのように報酬を分配することが公正な分配であるといえるか、つまり、各プレーヤーの協力はどの程度報酬獲得に寄与していると考えるべきか、という問題が生じます。シャープレイ値はこのような状況における公正な報酬分配、つまり貢献度計算方法の一つです。
算出方法
ここからは広告接触を協力ゲームに見立てた場合のシャープレイ値の具体的な算出方法について説明します。本来であれば広告接触の順序を考慮する必要がありますが、説明の簡単化のため順序を無視した広告の集合として扱います。
前提
前提として次のような広告経路とその経路をたどった上でのCV数があるとします。
| 広告経路 | CV数 |
|---|---|
| 広告A, 広告B, 広告C | 24 |
| 広告A, 広告B | 20 |
| 広告B, 広告C | 15 |
| 広告C, 広告A | 10 |
| 広告A | 6 |
| 広告B | 4 |
| 広告C | 2 |
各広告を協力ゲーム理論におけるプレーヤーとすると、広告経路はそのプレーヤーが協力関係を結んだ集合、CV数はその協力によって得られた報酬と考えることができます。
広告による報酬を$CV({広告})$と表し、広告の集合が協力することで得られる報酬の総和を表す特性関数$v$を次のように定義します。
$$v(S) = \sum_{s\subseteq S}CV(s)$$
$s$: 広告の集合$S$の部分集合
例)
$$v(A) = CV(A)$$
$$v(A,B) = CV(A) + CV(B) + CV(A,B)$$
$$v(A,B,C) = CV(A) + CV(B) + CV(C) + CV(A,B) + CV(B,C) + CV(C,A) + CV(A,B,C)$$
$$v(\varnothing) = 0$$
これを適用すると各広告経路の特性関数$v$は次のようになります。
| 広告経路 | CV数 | $v$ |
|---|---|---|
| 広告A, 広告B, 広告C | 24 | 81 |
| 広告A, 広告B | 20 | 30 |
| 広告B, 広告C | 15 | 21 |
| 広告C, 広告A | 10 | 18 |
| 広告A | 6 | 6 |
| 広告B | 4 | 4 |
| 広告C | 2 | 2 |
限界貢献度の算出
経路$S$は$v(S)$のCV数を獲得できるものとすると、これに広告$i$が加われば獲得できる値は$v(S\cup {i})$と表現できます。 この 2 つの値の差$v(S\cup {i}) − v(S)$を広告$i$の経路$S$に対する限界貢献度 (marginal contribution) と呼びます。
今回の場合、ある経路に広告Aを1つ追加した$v(S\cup\{i\})$は次のような4つのケースを考えることができます。
- 空集合に広告Aが加わったケース:$v(A) = 6$
- 広告Bに広告Aが加わったケース:$v(A,B) - v(B) = 30 - 4 = 26$
- 広告Cに広告Aが加わったケース:$v(A,C) - v(C) = 18 - 2 = 16$
- 広告B,Cに広告Aが加わったケース:$v(A,B,C) - v(B,C) = 81 - 21 = 60$
また、ある経路に広告を1つ追加する組み合わせは次のようになります。
- 空集合に広告を一つ追加:3パターン
- $\varnothing$ -> A
- $\varnothing$ -> B
- $\varnothing$ -> C
- 要素数1の経路に広告を一つ追加:6パターン
- A -> A, B
- A -> A, C
- B -> B, A
- B -> B, C
- C -> C, A
- C -> C, B
- 要素数2の経路に広告を一つ追加:3パターン
- A, B -> A, B, C
- B, C -> A, B, C
- C, A -> A, B, C
シャープレイ値の算出
いよいよ本題のシャープレイ値について紹介します。
シャープレイ値$\phi$とはこの組み合わせ数の逆数を重みとして限界貢献度の加重平均を取ったものと定義されます。
したがって広告Aのシャープレイ値$\phi(A)$は次のようになります。
$\phi(A) = \frac{v(A)}{3} + \frac{v(A,B) - v(B)}{6} + \frac{v(A,C) - v(C)}{6} + \frac{v(A,B,C) - v(B,C)}{3} = 29$
同様に広告B、広告Cのシャープレイ値を求めると次のようになります。
$\phi(B) = \frac{v(B)}{3} + \frac{v(A,B) - v(A)}{6} + \frac{v(B,C) - v(C)}{6} + \frac{v(A,B,C) - v(A,C)}{3} = 29.5$
$\phi(C) = \frac{v(C)}{3} + \frac{v(A,C) - v(A)}{6} + \frac{v(B,C) - v(B)}{6} + \frac{v(A,B,C) - v(A,B)}{3} = 22.5$
ここまでの処理を一般化した式が以下となります。
$$\phi_i(v) = \sum_{S\subseteq N\backslash \{i\}} \frac{|S|!(n-|S|-1)!}{n!}(v(S\cup\{i\})-v(S))$$
$n$ : 広告数
$S$ : 経路(広告の集合)
$|S|$ : 経路Sの要素数
シャープレイ値導入の成果
最後にシャープレイ値が他のアトリビューションモデルと比較してどのような数値になるのかを確認してみましょう。ファーストクリックモデル・ラストクリックモデルと比較したものが下記の表です。
| 広告A | 広告B | 広告C | |
|---|---|---|---|
| ファーストクリックモデル | 50 | 19 | 12 |
| ラストクリックモデル | 16 | 24 | 41 |
| シャープレイ値モデル | 29 | 29.5 | 22.5 |
シャープレイ値モデルでは最初の接点になりやすい広告Aと接触回数の多い広告Bの貢献度が大きく評価されているのに対し、最後の接点にはなりやすいが単独の接触だと獲得効率が悪い広告Cの貢献度が小さく評価されています。
ファーストクリックやラストクリックが恣意的な貢献度割り振りで過大評価を与えているのに対し、経路全体を考慮した公正な貢献度分配ができていると言えます。
おわりに
本記事では従来のアトリビューション分析の考え方と、協力ゲーム理論の一つであるシャープレイ値を適用した手法についてご紹介しました。今後はこのシャープレイ値モデルのさらなる精度向上と、貢献度に応じた自動予算アロケーションに向けたさまざまな取り組みを進めていく予定です。
私のチームで開発しているソリューションの他の記事も、ぜひご覧ください。
- 数千万ユーザーのビッグデータに機械学習モデルを適用するには(広告配信ソリューション実現の工夫紹介)
- 大規模言語モデルを使って広告文を自動生成する
- 機械学習でコンバージョンにつながるキーワードを予測する(学習データ不足でも推論可能にする工夫)
最後までお読みいただきありがとうございました。
こちらの記事のご感想を聞かせください。
- 学びがある
- わかりやすい
- 新しい視点
ご感想ありがとうございました

- 小林 岳
- データアナリスト
- Yahoo!広告のデータマーケティングソリューションを開発しています。



