こんにちは。サイエンス統括本部で検索モデリングを行っている今関です。クエリ処理や機械学習モデルの精度改善を通して、ヤフーのさまざまなサービスの検索体験向上に取り組んでいます。
みなさんは検定多重性という現象をご存知でしょうか? 本記事では、統計的検定の解釈に悪影響を与える検定多重性について定量的に分析を行った事例を紹介します。
まったく同じシステム同士のA/Bテストなのに、なぜか有意差発生
A/Bテストとはサービス改善を目的としたさまざまな施策がKPIに及ぼす影響を実験的に計測する手法で、施策発動対象のテスト群と比較対象のコントロール群にユーザやリクエストをランダムに割り付けてKPIの変化を見ます。ランダム化比較試験(RCT)と読み替えていただいても構いません(※厳密には異なるものであるという議論もあります)。
このA/BテストをYahoo!ショッピングで行った際に問題は起こりました。
きっかけはランダムにユーザを割り付けたX群, Y群, Z群の3群にまったく同じシステムを割り当ててA/Bテストしたことでした。目的はA/Bテストシステムにおけるユーザのランダム割り付け・集計・統計解析という一連の処理に問題がないことを確認することで、KPIである商品の購入率(CVR)に有意差は出ないはずのテストです。
ところが結果は以下の通り、X群に比べZ群が有意に増加してしまいました。
| 群 | CVR差(対X群) |
|---|---|
| X群 | - |
| Y群 | 有意差無し |
| Z群 | 有意に増加(※) |
※: 両側 p<0.10 (本A/Bテストにおける有意水準)
この場合まず疑うべきはA/Bテストシステムのどこかにバグがあることです。なんらかの理由で購入頻度の高いユーザがZ群にばかり割り当てられたり、統計処理にミスがありp値が実際よりも低く出てしまったりということがあれば、まったく差がない群の間で見かけ上CVRに有意差が出てもおかしくありません。
しかしながらいくら調査してもシステム上の問題は見当たりませんでした。
『多重性の問題』の可能性があるも、それだけとも言い切れない
本A/Bテストにシステム的問題が見当たらない一方、統計手法的には1点問題がありました。それは検定多重性の問題です。検定多重性とは、3群以上の比較を行う際、本当は有意差が無いはずなのに有意差ありとなってしまう確率が2群の時よりも上がってしまう現象です。
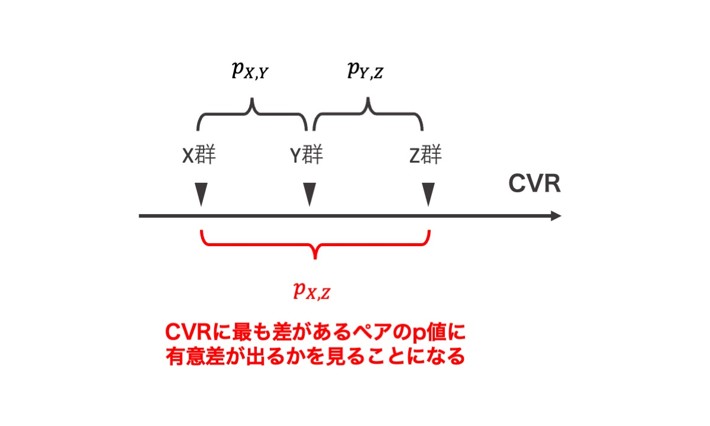
このA/Bテストシステムは2群間での比較を前提にt検定で実装されており、多重検定には対応していませんでした。しかしながら今回は諸般の事情により対等な3群間でテストしており、(X,Y), (X,Z), (Y,Z)の3ペアでの比較が行われ、最も差が大きいペアのp値を見ることになっていました。
まったく差がないシステムのA/Bテストで p<0.10 の有意差が出る確率は理論上10%ですが、3ペアで最も差が大きい(すなわちp値が最も小さい)p値を見る場合は10%よりも大幅に高くなると考えられます。
それでは『多重性が原因で、有意差は偶然でした』で済ませられるかというと、そういうわけにもいきません。『確かに有意性が出やすい事情はあったものの、だからと言ってA/Bテストシステムに問題がないと言えるだろうか』という疑問が残ります。A/Bテストシステムの信頼性が疑わしい状態では今後の意思決定が困難になるため、疑惑の解消は急務でした。
そこで単に多重性により有意差が出やすいという定性的な考察ではなく、多重性以外に有意差が出やすくなる偏りが本当になかったかということを知るため定量的に掘り下げることにしました。
分析の流れは以下の通りです。
- 多重性によりどの程度有意差が出やすくなっていたのかをシミュレーションで定量化
- 本番システムで同様のA/Bテストを繰り返し、有意差の頻度が1.の結果と一致するかを確認
まずは1.の多重性の影響を定量化した分析から紹介します。
A/Bテストシミュレーションによるp値の偏りの定量化
多重性によって有意差はどの程度出やすくなっていたのでしょうか。単純に3ペアなので3倍……ではありません。(X,Y), (X,Z), (Y,Z)の3ペアの中に群の重複があるので3つのp値が独立ではないためです。
今回は解析的に解くのが難しいと考えられたことから、シミュレーションにより実験的に求めることにしました。
説明のために手順を簡略化したイメージを以下に示します。まず本A/Bテストの割り付け単位であるユーザごとに購入のログを集計します。(※ここで取り扱っているデータは、プライバシーポリシーの範囲内で取得したデータを個人が特定できない状態に加工しています。また数値は擬似データで、実際の値とは無関係です。)
| ユーザ | 商品の購入数 |
|---|---|
| Aさん | 3 |
| Bさん | 0 |
| Cさん | 2 |
| Dさん | 1 |
| … | … |
次にユーザリストからサンプリングしてA/Bテストと同じ割合で割り付けて仮想的なA/Bテストとみなします。これを繰り返し行った後にそれぞれの試行でp値を計算し最小のものを残すことで、p値の経験分布を得ることができます。
ランダムに割り付けたユーザ
| 仮想的な群 | ユーザ(試行1) | ユーザ(試行2) | … |
|---|---|---|---|
| X群 | Aさん, Bさん, … | Cさん, Aさん, … | … |
| Y群 | Cさん, Aさん, … | Bさん, Bさん, … | … |
| Z群 | Dさん, Dさん, … | Aさん, Dさん, … | … |
| 3ペアで 最小のp値 |
0.11 | 0.34 | … |
表を見てバケット内・バケット間ともにユーザの重複があることに気づきましたでしょうか? これはブートストラップサンプリングと呼ばれる、復元抽出により再標本化をする手法です。直感的には非復元抽出の方が実際のA/Bテストの条件に近そうですが、有限母集団に対する非復元抽出では偏りが生まれることが知られており[1]、ここでは復元抽出が適切です。
偏りなく検定ができていれば、p値はその定義から0〜1の範囲を取る一様分布であることが期待されます[2]。実際に表の設定を変更してX, Yの2群のみへ割り付ける設定で10000試行シミュレーションすると、p値は以下のようにほぼ一様な分布を描きました。
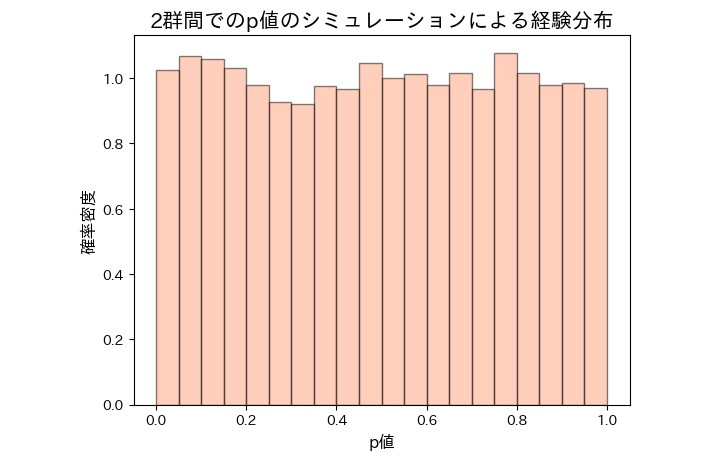
またこの結果は、2群間であれば偏りなく統計処理できているということを示してもいます。有意水準である p<0.10 となった試行の割合は約10.5%となり、想定される10%にほぼ一致する割合でした。
続いて3群に割り付けた結果が以下の通りです。想定通り、多重性によりp値が低い領域に偏っていることがわかります。
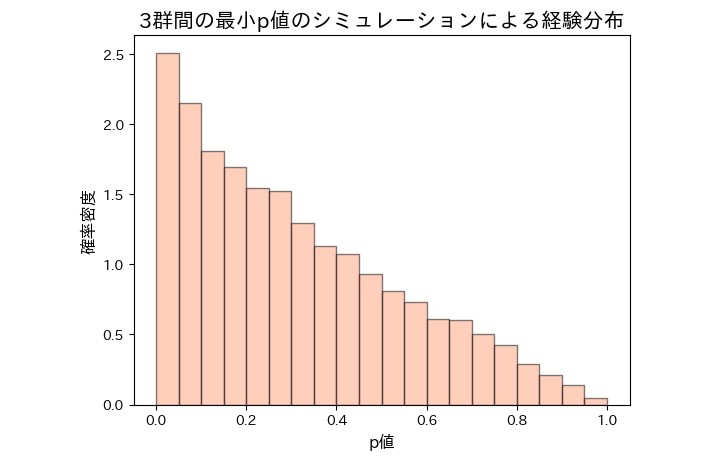
p<0.10 となった割合は約23.3%で、2群の時の2.3倍も有意差が出やすくなっていたということがわかりました。
本番システムでシミュレーション結果との一致確認
さて、シミュレーションで有意差が約2.3倍出やすくなっていることがわかりましたが、これだけでは冒頭の有意差が偶然であるとは言えません。そこで本番のシステムでなんどもA/Bテストを回し、本当に有意差が出る確率が23%に近づくことを確かめました。
結果は以下の通りです。再A/Bテストでは2〜4回目のいずれも有意差が出ませんでした。この時点で有意差の確率は1/4=25%となり、シミュレーションとほぼ一致しました。多重性の問題を除けば、A/Bテストシステムに有意差が出やすくなるような偏りはなかったことを示唆する結果となっています。
A/BテストにおけるCVR(対X群)
| 群 | 2回目 | 3回目 | 4回目 |
|---|---|---|---|
| X群 | - | - | - |
| Y群 | 有意差無し | 有意差無し | 有意差無し |
| Z群 | 有意差無し | 有意差無し | 有意差無し |
もちろん一致といっても4回という試行回数は少なく、本来は10回・20回と回して検証するのが望ましいでしょう。しかしながら本番システムでのA/Bテスト実施は実装や運用コストが少なからずかかり、しかも実施中は他のA/Bテストができません。
そこでここまでの結果をもってA/Bテストシステムに大きな問題はないだろうという結論でステークホルダーと合意を形成しました。その後A/Bテストでシステムを疑うような結果が出ることはなく、円滑な施策検証ができています。
また今回の分析を踏まえ、これまで明確に意識していなかった検定多重性の扱いについてステークホルダーと整理する機会につなげることもできました。
おわりに
本記事では検定の偏りを定量化するための手法としてブートストラップサンプリングによるA/Bテストシミュレーションを紹介し、それを検定多重性の影響の定量化に用いた分析事例を紹介しました。
本手法は今回のような特殊なケースだけでなく、一般にp値が一様分布を示すか見ることで統計的検定の実装の正しさを確かめることにも利用できます。ご利用のA/Bテストプラットフォームにおける検定の実装に不安がある場合、シミュレーションでp値が一様分布を描くか確認してみることをオススメいたします。
参考文献
- [1] 松原望, 縄田和光, 中井検裕 (1991) 統計学入門 基礎統計学I. 東京大学出版会.
- [2] R. Kohavi, D. Tang, Y. Xu著, 大杉直也訳 (2021). A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実験とは. ドワンゴ.
こちらの記事のご感想を聞かせください。
- 学びがある
- わかりやすい
- 新しい視点
ご感想ありがとうございました




