こんにちは。Yahoo! JAPAN研究所でインタラクション分野の研究をしている山中です。
コロナ渦の昨今、インタラクション領域ではユーザ実験もままならない状況でした。できることを見いだそうとした過程で、「クラウドソーシングを活用したリモートでのユーザ実験」の知見を蓄積し、論文という形で公開できました。不自由な状況下でも、オンラインでの大規模ユーザ実験という新たな可能性につながりました。
今回の記事では、クラウドソーシングに関する国際会議HCOMP 2021で発表した研究成果[1]を解説します。
Yahoo! JAPAN研究所の活動と冊子の紹介
Yahoo! JAPAN研究所では、国際学会での論文発表を目指した活動を精力的に行っています。特に論文採択難度が高い学会はトップカンファレンスと呼ばれ、採択率が全投稿論文中の2割程度になることもあります。
できるだけ多くの方にわれわれの研究成果を知っていただきたいのですが、英語で10ページを超える論文もあるため、内容を知りたくても気軽に読むのは難しいと思います。そこでYahoo! JAPAN研究所では、トップカンファレンスに採択された論文を各1ページで解説した冊子を作成しています。2021年に発表された論文をまとめた冊子はこちらです(PDFファイル:論文紹介冊子”Yahoo! JAPAN Selected Papers in 2021”)。また、2017~2020年の冊子もダウンロード可能なので、こちらもぜひご覧ください(冊子のまとめページ)。
今回のこの記事の研究成果も冊子に掲載されています。
インタラクション分野におけるクラウドソーシングの活用
近年ではクラウドソーシングを活用した研究が多く発表されていますが、画像のアノテーションやアンケートの回答に利用するものが多いです。これに対してインタラクション分野では、ユーザインタフェース(UI)の操作時のデータを大量に収集する目的で活用されることがあります。たとえばマウスカーソルから最も近くにあるボタンをクリックできるようにしたバブルカーソルという操作方法を使うと、通常のマウス操作よりも所要時間が短くなり、かつミスクリック率も低くなることをクラウドソーシング実験で示した論文が2013年に発表されています[2]。
このバブルカーソル自体は2005年に発表されており、大学研究室(ラボ)で12名を対象にユーザ実験をしたものでした[3]。一方で2013年の研究では、実験参加者数を123名と多くしたことで有意差を検出しやすくなったため、「提案手法を使うことでパフォーマンスが向上した」と主張したい研究にはクラウドソーシングが適していると述べられています。ここでのパフォーマンスというのは、UIを操作したときの成績を意味します。たとえばボタンをクリックするまでに要した時間や、ミスクリック率などが代表的なパフォーマンス指標です。
クラウドソーシングを活用したUI研究論文には、パフォーマンスを推定するモデルを評価したものも多くあります。ボタンの大きさや配置などからクリック時間を予測するモデル[4]や、スマートフォンで画面をスクロールする距離に応じて所要時間を推定するモデル[5]などがあります。
これらの先行研究の多くは「ラボ実験とクラウドソーシング実験では同じ結論が得られる」と述べています。前述の研究[4,5]で検証されているパフォーマンス推定モデルも、それ以前にラボ実験で妥当性が確認されているものが使われています。もちろんクラウドソーシングのメリットとして代表的なのは、より小さな労力で大人数の参加者を集められることや、それによって有意差を検出しやすいことです。しかし、あくまでも「ラボ実験をクラウドソーシングに置き換えても問題なく結果を得られる」という位置付けの論文が多かったのです。
これに対して私は、クラウドソーシングで実験することのメリットが大きくなるような研究テーマを模索していました。そこで着目したのが、ボタンの大きさに基づいてマウスクリックのミス率を推定するモデルです。これは私が以前に投稿したYahoo! JAPAN Tech Blogの記事で解説した、スマートフォンのタップ成功率を予測するモデルをマウス操作で追試したものです。このモデルによって、「ボタンがこの大きさならミスクリック率は5%未満になるから適切だ」などと操作性に基づいてアプリやウェブページがデザインできるようになります。
ミスクリック率の推定モデル
下の図のように、左右の棒状のボタンを往復してクリックし、1クリックあたりの所要時間とミス率を測定します。ボタン同士は $A$ ピクセルだけ離れていて、ボタンの幅は $W$ ピクセルです。
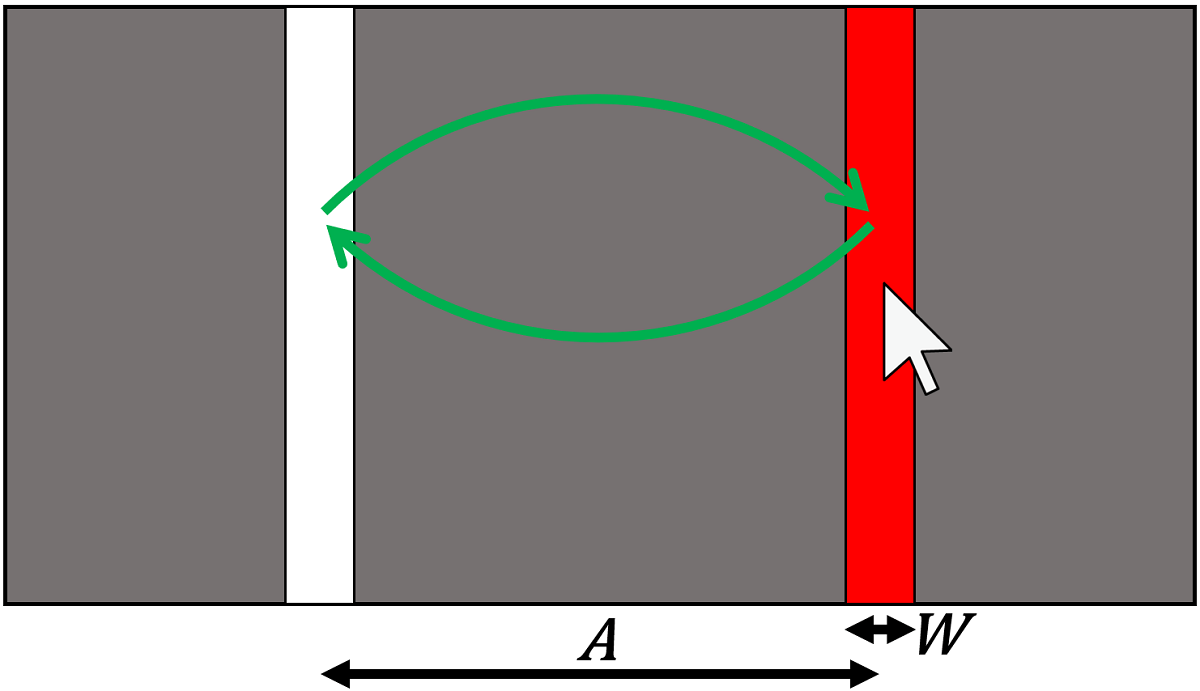
距離 $A$ は3種類、幅 $W$ は8種類用意したので、合計で24種類のボタン条件があります。これら24条件を5往復(= 10クリック)して成績を記録したので、あるボタン条件(たとえば $A=300$ ピクセル、$W=26$ ピクセルのボタン)について2回ミスクリックすると、ミス率は20%となります。
さて、ボタンの大きさに基づいてミスクリック率を推定するのは2つのステップに分かれます。
- ボタンの大きさに基づいて、クリック座標のX軸方向のばらつき(標準偏差 $\sigma_x$)を推定する。
- クリック座標のばらつき $\sigma_x$ に基づいて、クリックがボタン外に出てしまう確率を求める。
下の図のように、幅 $W$ がさまざまなボタンを何度もクリックしてみます。ばらつき $\sigma_x$ はボタンの幅 $W$ が大きくなるにつれて大きくなり、またクリック座標はボタンを中心とした正規分布になります。
- (1): $\sigma_x = a + b \times W$ …… $a$ は切片、$b$ は傾き。ばらつき $\sigma_x$ はボタンの幅 $W$ の1次関数になる。
- (2): $X \sim N(\mu_x,\sigma_x^2)$ …… クリック座標 $X$ は正規分布する(平均 $\mu_x$、分散 $\sigma_x^2$)
これでボタンの幅 $W$ に応じてどのくらいクリック座標がばらつくかを推定できるようになりました。次に、このばらつき $\sigma_x$ から、クリック座標がボタンの外に出る確率、つまりミスクリック率を推定します。下の図のように、クリック座標がボタンのX軸方向の範囲 $W$ に入るかどうかを考えます。
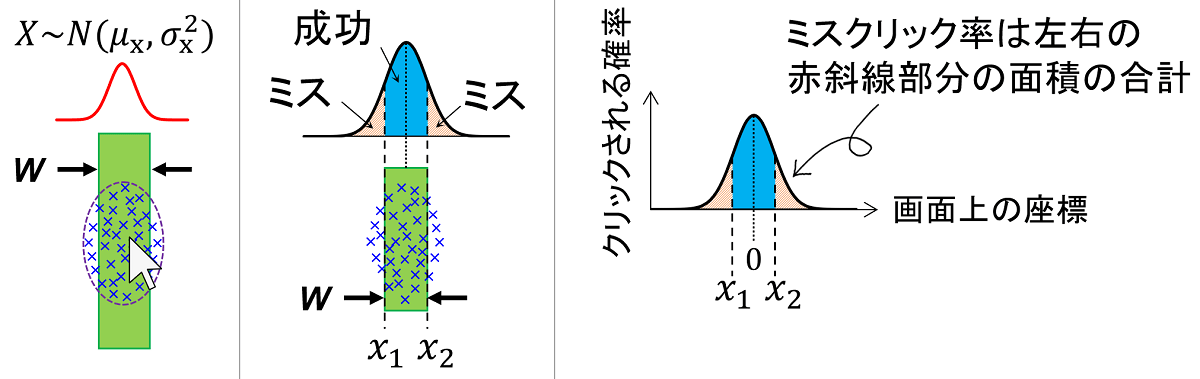
ボタンの中心を座標 $x=0$ とすれば、ボタンの範囲は $\{-\frac{W}{2} \le x \le \frac{W}{2}\}$ となります。また、クリック座標の平均 $\mu_x$ はおおよそボタンの中心と一致することが知られているので $\mu_x=0$ となります。クリック座標はX軸方向に正規分布するはずなので、クリックがボタンの範囲に入らない確率 $P(E)$ は、
- (3): ミスクリック率 $P(E) = 1-\mathrm{erf}\left(\frac{W}{2\sqrt{2}\sigma_{x}}\right)$
となります。$\mathrm{erf}(\cdot{})$ はガウスの誤差関数です。
クラウドソーシングでのユーザ実験
Yahoo!クラウドソーシングで384名のマウス利用者にこのクリックタスクを行ってもらいました。今回の実験では、Windowsを利用しているクラウドワーカーに実行ファイル(.exe拡張子の実験プログラム)を配布し、タスクが終わった後に生成される実験ログをサーバーにアップロードしてもらう手順をとりました。まず上記の式(1)の結果は下の図のようになりました。
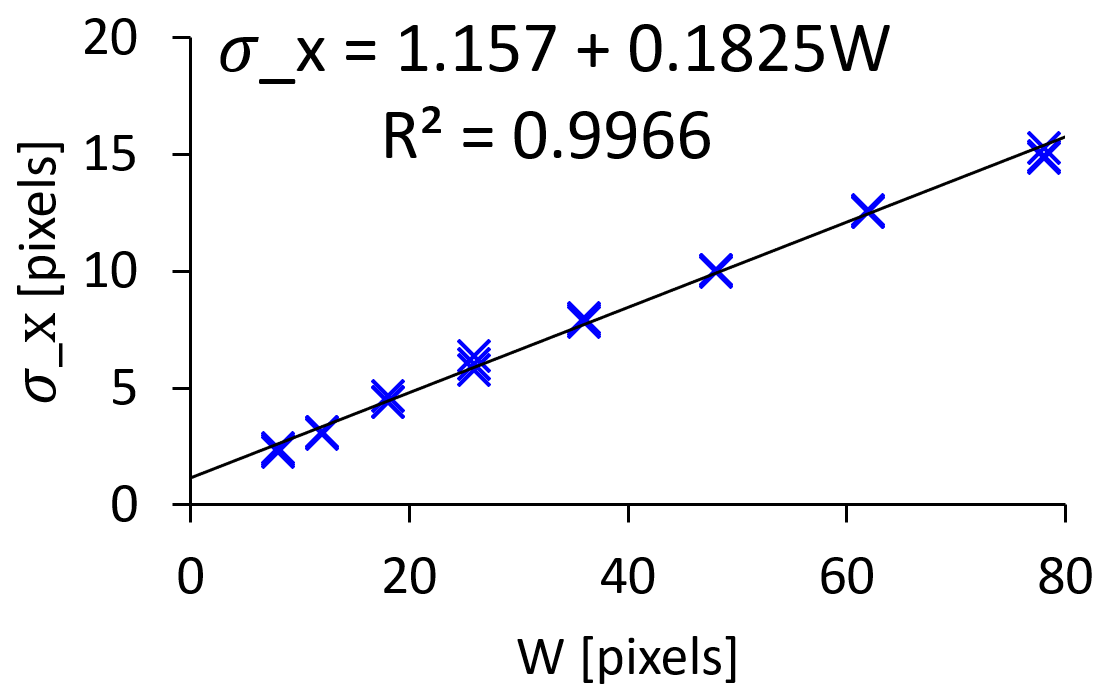
$R^2$ の値が0.9966となっており、「ボタンの幅 $W$ が大きくなるにつれて、1次関数的にクリック座標のばらつきが大きくなる」と言えそうです。次に、式(2)で予測したミスクリック率と、実際に測定したミスクリック率を並べたものが下の図です。
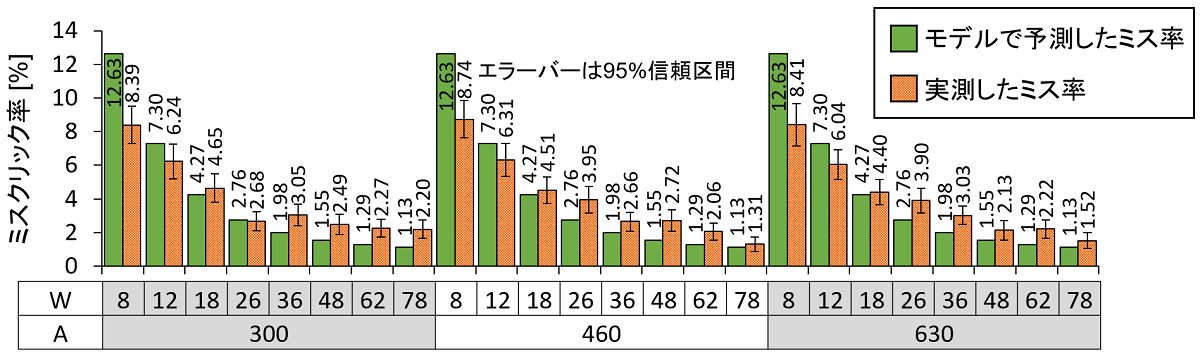
モデルの予測精度を調べるために一つ抜き交差検証をしたところ、予測値と実測値の相関(決定係数 $R^2$)は0.9529、予測値と実測値の差の絶対値は平均で1.272%でした。
実験参加人数とクリック数がモデルの予測精度に与える影響
そもそもミスクリックは、上の図からも分かるようにほんの数%の確率でしか観測できない事象です。ということは、人数やクリック数が少ない場合は、1回のミスクリックが全体のミス率を大きく変化させてしまい、(モデルが正しかったとしても)予測値との差が大きくなってしまう可能性があります。
今回は384名のクラウドワーカーに参加してもらったため、1つのボタン条件について合計で10回クリック×384名=3840回ものクリックを記録していたことになります。よって1回ミスクリックをするごとに、全体のミスクリック率を $1/3840 \times 100\% = 0.026\%$ だけ上昇させることになります。一般的なラボ実験では、より小人数の参加者に繰り返しクリックをしてもらってミス率を計測する場合が多いです。たとえば12名に20回クリックをしてもらうと、1回のミスが0.42%に相当します。
クラウドソーシングで大人数を集めることのメリットは、このようにレアにしか発生しない事象を精度よく計測し、確率予測モデルを適切に評価できることだと考えました。これを検証するために、以下の2項目を追加で分析しました。
- もし人数を384名から減らしても、モデルでミスクリック率を予測できるか?
- もし1名あたりのクリック数を10回から減らしても、モデルでミスクリック率を予測できるか?
たとえば、384名のうちランダムで20名を選び出し、その人たちの最初の5回分のクリックだけを分析に使って、これまでと同様にミスクリック率の予測値と実測値(およびそれらの相関である $R^2$)を計算します。さらに、どの20名を選び出すかのランダムさの影響を減らすために、この計算を100回行い、その平均の $R^2$ を求めます。この選出人数を10名から320名まで変更し、さらにクリック数を2回から10回まで変えたときの $R^2$ が下の図です。
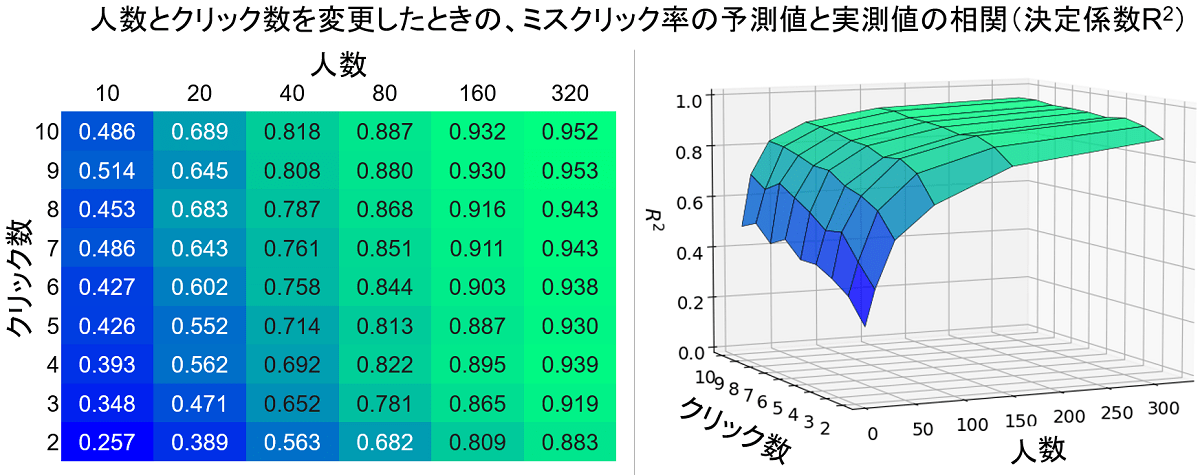
たとえば上図の左側で、人数が20名、クリック数が5回の箇所を見ると、$R^2 = 0.552$ であり、モデルではうまくミスクリック率を予測できていないことがわかります。しかしクリック数が同じ5回でも、人数を320名まで増やせば $R^2 = 0.930$ になり、高精度に予測できることが分かります。
この表を3Dグラフで表示したのが上図の右側です。人数が少ないか、繰り返しのクリック数が少ないときには明らかにモデルの予測精度が落ち込んでいることが分かります。よって、モデルが適切なものかをジャッジするには、かなり多くの実験参加者数を確保するか、あるいは小人数に長時間同じタスクを繰り返してもらって大量のクリックデータを集める必要があります。
クリックの所要時間を推定するモデルとの比較
ボタンをクリックする時間 $T$ を予測するモデルとして、フィッツの法則という次の式(4)がよく知られています。
- (4): $T = a + b \log_2\left({\frac{A}{W}+1}\right)$
クリックしたいボタンまでの距離 $A$ が長いほど時間がかかり、また幅 $W$ が小さいほど慎重な操作が必要なので長時間になるという関係があります。この式(4)の結果は次の図のようになりました。
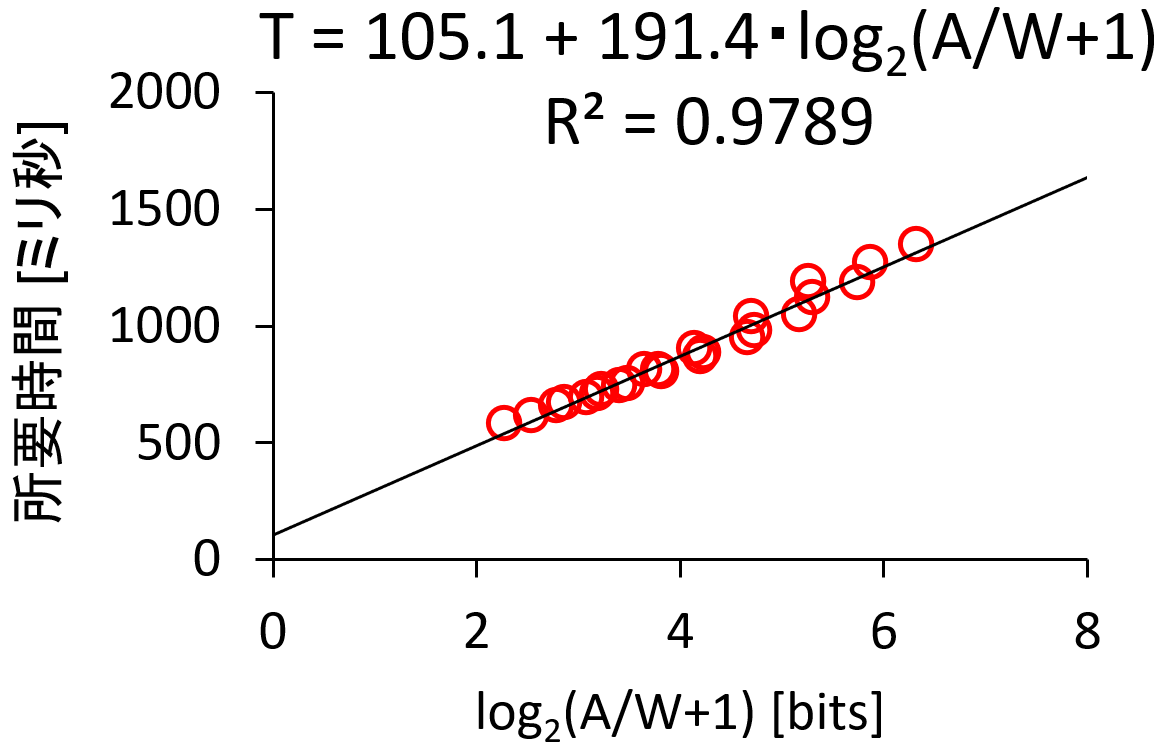
これも $R^2=0.9789$ と高い適合度を示しています。ミスクリック率の分析と同様に、人数とクリック数を変更してモデルの予測精度を調べたのが下の図です。
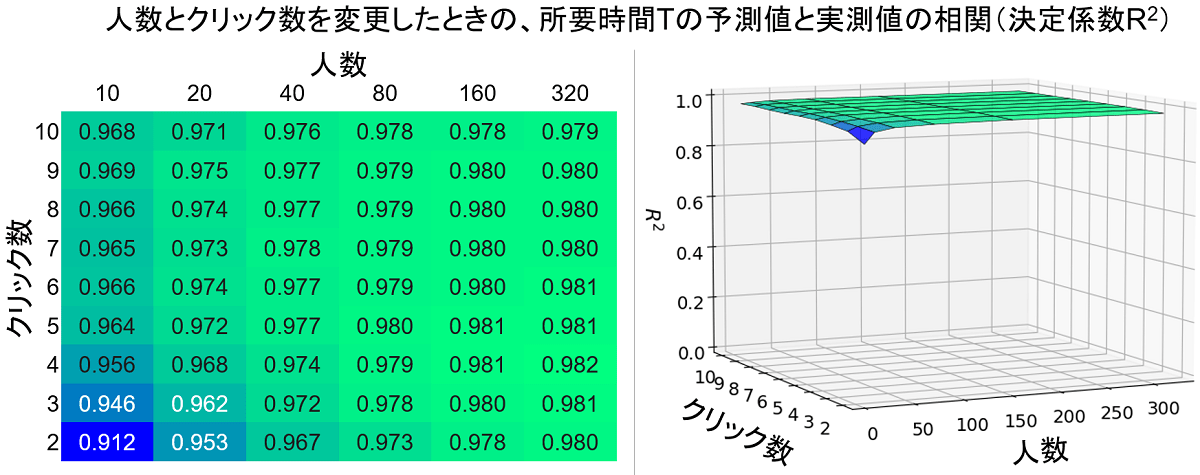
ミスクリック率の場合とは異なり、人数やクリック数が少なくても高精度に所要時間Tを予測できると言えそうです。たとえば10名が各ボタン条件について2回ずつクリックしただけでも、$R^2$ の値は0.9を超えています。逆に、人数を増やしていっても、あまり予測精度を向上させるような恩恵は受けにくいとも言えます。仮に10名に10回クリックしてもらった場合は $R^2=0.968$ ですが、これを320名まで増やしても $R^2=0.979$ までしか上昇せず、わずか0.011ポイントの差です。
レアな事象のモデル評価にはクラウドソーシングが有効
以上のように比較してみると、データサイズを大きくする(人数とクリック数を増やす)ことで、ミスクリック率モデルの予測精度をより適切に評価できることが分かります。逆に言えば、もし小人数で実験して予測精度が低かったとしても、それはモデルが間違っているのではなくデータが少ないだけの可能性が残されています。
なぜミスクリック率モデルと所要時間モデルでこのような差が出たのでしょうか。前述したように、ミスクリック率はあくまで全体のうちの何%がミスだったのか、その割合が成績になります。そして1つのボタン条件について1人10回だけクリックするのですが、結果を見るとミスクリック率は10%を下回ることも多いです。つまり、10回クリックしたときに1回もミスを起こさないこともあるのです。たとえば9回目のクリックまでミスがなければその時点まではミス率0%、10回目でようやくミスをしたら急に10%に増える、というように極端な変わり方をします。このようなレアな事象の確率モデルを適切に評価するには、データサイズを大きくするのが直接的に効果があります。
一方で所要時間は、毎回のクリックでデータを計測できます。いわばミスクリック率よりもデータサイズが大きくなるために、小人数・小クリック数でも問題ありませんでした。クラウドソーシングを利用した場合でもモデルの評価は適切に行えていますが、これは十数名程度のクラウドワーカーを雇うだけで十分に効果的であり、今回のように300名以上を募集するメリットは比較的小さいと言えるでしょう。
こういった違いがあるため、どのようなパフォーマンス指標をモデル化するかによって、クラウドソーシング実験のメリットの大きさが変わってくることが分かりました。レアな事象のモデル評価をするのであれば、数百人、あるいは千人以上のパフォーマンスデータを短期間に収集可能なクラウドソーシングの恩恵を大きく受けられるはずです。
おわりに
同じタスク・同じデータセットを使っているにも関わらず、研究テーマによってはクラウドソーシングの利点が顕著になるというのは、私にとって大きな発見でした。実は、新型コロナウイルスが流行しはじめたころから対面でのユーザ実験ができなくなり、代替方法としてクラウドソーシングに力を入れたという経緯があります。もし状況が落ち着いたらまた全てのユーザ実験を対面で行う計画だったのですが、今回の研究結果を見て、テーマによっては今後もクラウドソーシングを活用し続けようと考えるようになりました。もちろん、ラボ実験でも数百名規模の参加者を集めればクラウドソーシングと同様の結果を得られるはずですが、それは現実的な選択肢とは言えません。
今回のクラウドソーシング実験では、クラウドワーカーに実行ファイルを配布する方法をとりました。その他の実験方法として、ウェブサイト上で動作するような実験ページを構築してクラウドワーカーにアクセスしてもらう方式や、スマートフォンアプリを公開してインストールしてもらう方式などがあります。研究目的によってはクラウドワーカーの実験環境(PCやスマートフォンの機種など)を限定したい場合もありますが、上記のように特定のOS利用者だけ募集することも可能ですし、またにスマートフォンの場合でも「iPhone11以降の機種を持っているクラウドワーカー向け」などと属性を指定することもあります。このように対象ユーザを絞っても数百名規模のデータが数日で集められることは大きなアドバンテージであり、今後もインタラクション分野でクラウドソーシングの活用は広がっていくと考えています。
参考文献
- [1] Yamanaka. Utility of crowdsourced user experiments for measuring the central tendency of user performance to evaluate error-rate models on GUIs. In Proc. of HCOMP 2021. pp. 155-165.
- [2] Komarov, Reinecke, and Gajos. Crowdsourcing performance evaluations of user interfaces. In Proc. of CHI 2013. pp. 207-216.
- [3] Grossman and Balakrishnan. The bubble cursor: enhancing target acquisition by dynamic resizing of the cursor’s activation area. In Proc. of CHI 2005. pp. 281-290.
- [4] Findlater, Zhang, Froehlich, and Moffatt. Differences in crowdsourced vs. lab-based mobile and desktop input performance data. In Proc. of CHI 2017. pp. 6813-6824.
- [5] Schwab, Hao, Vitek, Tompkin, Huang, and Borkin. Evaluating pan and zoom timelines and sliders. In Proc. of CHI 2019. No. 556, pp. 1-12.
こちらの記事のご感想を聞かせください。
- 学びがある
- わかりやすい
- 新しい視点
ご感想ありがとうございました
- 山中 祥太
- Yahoo! JAPAN研究所
- インタラクション分野、特にユーザインタフェースの操作性に関する研究をしています。



