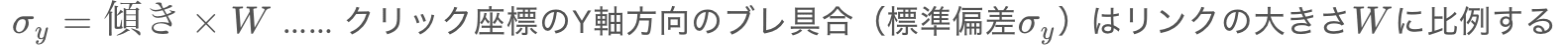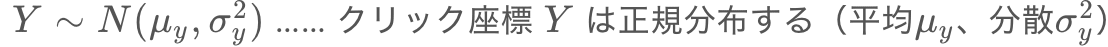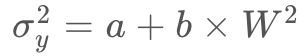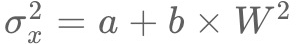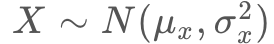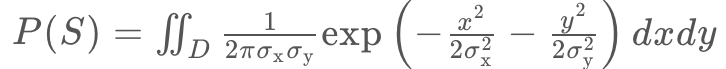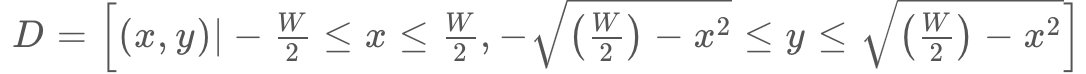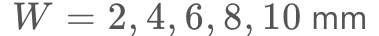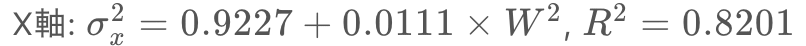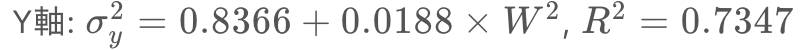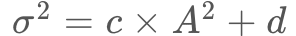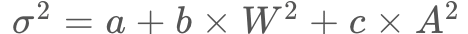こんにちは。Yahoo! JAPAN研究所で快適に操作できるUIを作るといったインタラクション分野の研究をしている山中です。
この記事では、リンクやボタンの大きさに基づいてタップの成功率を推定するモデルについて解説します(国際会議ISS 2020で発表した研究成果です [1])。
このモデルを活用すると、アプリやウェブページのデザインをするさいに、デザイナーが経験的にボタンやリンクの大きさを設定するのではなく、「リンクがこの大きさであれば95%の確率でタップできるから十分だ」などと操作性に基づいてユーザインタフェース(UI)を設計できるようになります。
タップの成功率を推定できると何が嬉しい?
スマートフォンやタブレットPC向けのアプリやウェブページの画面をデザインするとき、あまりにも小さすぎるボタンは操作性が悪いので避けるべきだと言われています。マウスカーソルでの操作と比較すると、タッチ操作はボタンを選択するときにミスタップすることが多いと言われています。そのためタッチUIではボタンを大きくするべきだとされており、たとえば「正方形のボタンであれば、一辺が17.5 mmあれば快適に操作できる」というデータがあります [2]。しかし、これはATMや券売機のような大型のタッチスクリーンを想定した研究でした。
スマートフォン用のウェブページなどでは、1つの画面に多くのボタンやリンクを配置したいことがあり、上記のように各々のボタンに17.5 mmもスペースを割けないことがあります。このとき、対応策として考えられるのは(1)ボタンのサイズを小さくして、1画面内に多くのボタンを配置するか、(2)ボタンの大きさを確保したままページを縦に長くする、というのが考えられます。しかし(2)では、ページの下部にあるボタンを選択するには何度もスクロールしなければならず、ユーザに追加の負担を強いてしまいます。よって、可能であれば1画面内に多くのボタンを収めたいところです。
上記(1)のボタンを小さくする方法を採用する場合に、どの程度サイズを確保すれば良いのかが問題になります。実際のサービスで検討する中には「このボタンはほとんど使用されないので、ミスタップ率が高くても問題ない」「このリンクはページ内で一番使われるので、タップ成功率が99%以上になるようにしたい」などと、画面内のスペースを割くにあたっての優先度が異なることがあります。
そういう時に、ボタンやリンクの大きさに基づいてタップ成功率を推定するモデルが役立ちます。このモデルを使い、「このハイパーリンクは高さが4.3 mmなので、88.2%の確率でタップが成功するはず」などと算出できれば、数値に基づいて「このままではミスが多すぎるから、あと1 mmだけ大きくしてみよう」「ほとんど使われることがないリンクなので、空いているスペースは他のリンクを大きくするために使おう」などとチーム内で議論できます。
このモデルは、あくまでもデザイナーが画面を設計するうえでの指標の1つとして、タップを正確にできるかどうか推定してくれるというものです。このタップ成功率推定モデルが画面デザインの良さなどを評価してくれるわけではないことにご注意ください。
どのようにタップ成功率を推定モデルを作るのか?
ボタンやリンクの大きさに基づいてタップ成功率を推定するのは2つのステップに分かれます。
- ボタンの大きさによってタップ座標の分散を推定する。
- タップ座標の分散から、タップがボタン内に入る確率を求める。
ボタンの大きさによってタップ座標の分散を推定する
まずはタッチ操作ではなく、マウスカーソル操作におけるクリック座標の分散についてお話しします。幅は十分で、高さが様々なリンクを複数回クリックするとします。すると数%の割合でミスクリックが発生しますが、十分に時間をかけてよいのであれば、仮に1ピクセルの細い線であってもクリックできるはずです。
そしてポイントなのが、Y軸方向のクリック座標のブレ具合(標準偏差 ![]() )は、リンクの高さ
)は、リンクの高さ![]() が大きくなるにつれて大きくなり、クリック座標はリンクを中心とした正規分布になるという性質です。
が大きくなるにつれて大きくなり、クリック座標はリンクを中心とした正規分布になるという性質です。
この関係を模式的に表したのが次の図です。いま、 の関係から、分散
の関係から、分散![]() はリンクの大きさの2乗(
はリンクの大きさの2乗(![]() )に比例するはずなので、
)に比例するはずなので、
としたときの切片![]() がほぼゼロになっています。
がほぼゼロになっています。
しかしタッチ操作のUIではこれと大きく異なる結果が得られます。もし「時間をかけてもいいので、高さ1 mmのリンクを正確にタップしてください」と言われたとしても、マウスカーソルと違って正確にタップできるとは限りません。小さいリンクは指で隠れてしまいますし、ユーザ自身も自分の指がどの座標をタップするのか事前に分からないからです。さきほどと同様の図を描くと下のようになります。
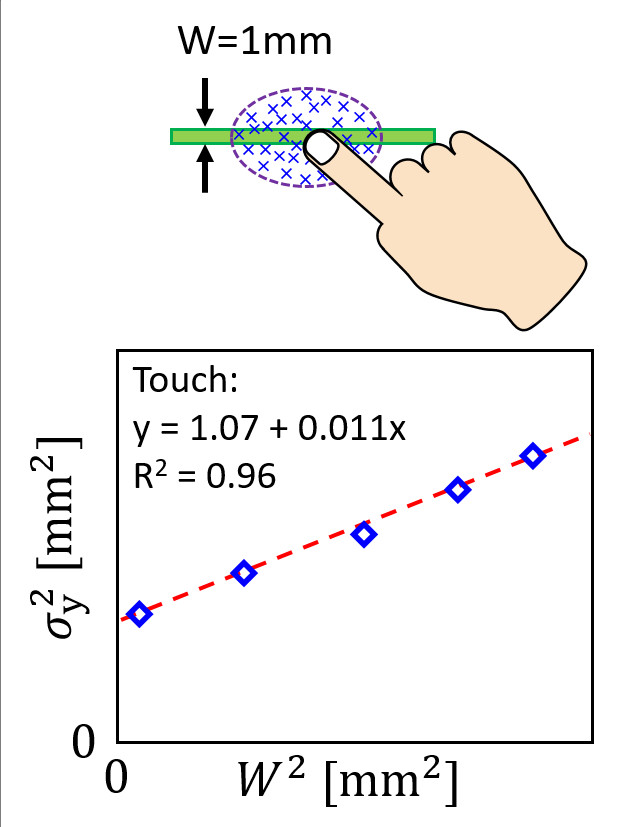
一番の違いは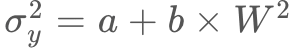 の切片が大きい点です。ただ、リンクの大きさ
の切片が大きい点です。ただ、リンクの大きさ![]() が大きいほどタップ座標のブレ具合が大きくなる、という関係はマウスカーソル操作と同様です。よって、もし数種類のリンクの大きさ
が大きいほどタップ座標のブレ具合が大きくなる、という関係はマウスカーソル操作と同様です。よって、もし数種類のリンクの大きさ![]() でタップ座標の分散
でタップ座標の分散![]() を測定すれば、この回帰直線によって未知の
を測定すれば、この回帰直線によって未知の![]() についても分散が推定できます。たとえば、
についても分散が推定できます。たとえば、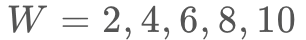 mmの5種類のリンクを使ってタップ座標の分散
mmの5種類のリンクを使ってタップ座標の分散![]() を測定して回帰直線を求めておけば、仮に
を測定して回帰直線を求めておけば、仮に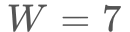 mmのリンクをタップした場合の分散もこの回帰直線から算出できるはずです。
mmのリンクをタップした場合の分散もこの回帰直線から算出できるはずです。
さて、ここまでは横に長いリンクを想定して、Y軸方向の分散だけを考えてきましたが、実はX軸方向についてもタップ座標は同様の性質になることが知られています。たとえば直径![]() mmの円形のボタンを選択するのであれば、以下のようになります。
mmの円形のボタンを選択するのであれば、以下のようになります。
ただし、切片![]() と傾き
と傾き![]() はX・Y軸でそれぞれ異なります。
はX・Y軸でそれぞれ異なります。
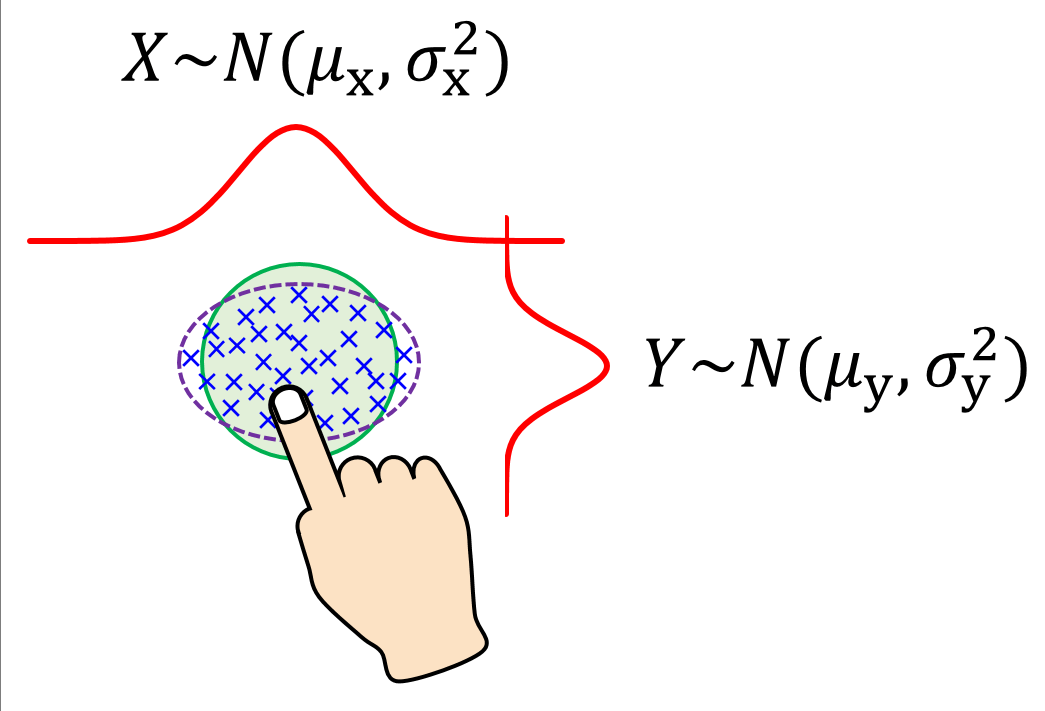
Y軸座標のときと同様に、数種類の直径![]() で何度もボタンをタップすれば、X座標についても回帰直線で分散
で何度もボタンをタップすれば、X座標についても回帰直線で分散![]() を推定できるようになります。
を推定できるようになります。
タップがボタン内に入る確率を求める
ここまでで、ボタンの大きさ![]() に応じてどのくらいタップ座標がブレるのかをX・Y軸方向について推定できるようになりました。次に、これらの分散
に応じてどのくらいタップ座標がブレるのかをX・Y軸方向について推定できるようになりました。次に、これらの分散![]() と
と![]() から、タップ座標がボタンの中に入る確率、つまりタップ成功率を推定したいです。下の図のように縦方向に長いボタンがあり、タップ座標がX軸方向の範囲
から、タップ座標がボタンの中に入る確率、つまりタップ成功率を推定したいです。下の図のように縦方向に長いボタンがあり、タップ座標がX軸方向の範囲![]() の中に入るかどうかを考えます。
の中に入るかどうかを考えます。
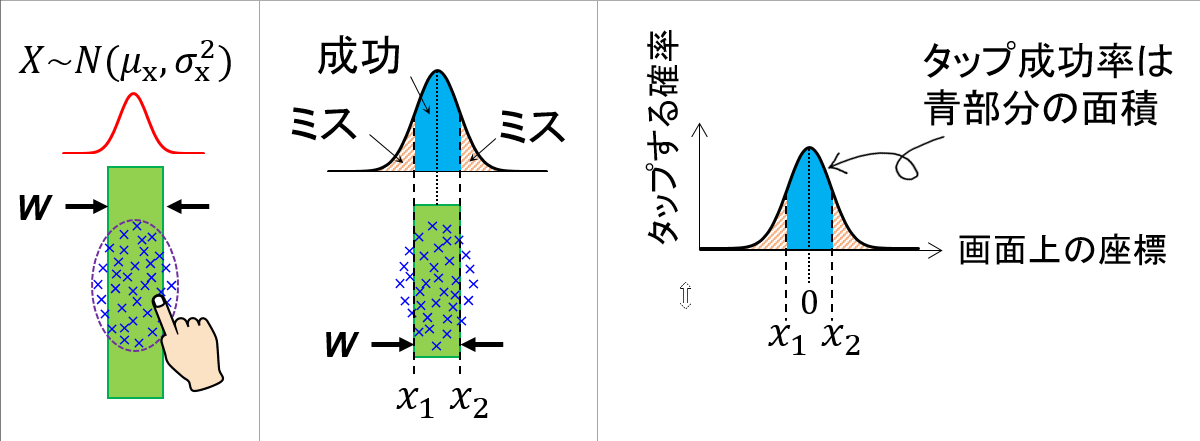
いま、ボタンの中心を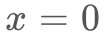 とすれば、ボタンの範囲は
とすれば、ボタンの範囲は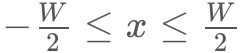 となります。また、タップ座標の分布のうち、平均
となります。また、タップ座標の分布のうち、平均![]() はおおよそボタンの中心と一致することが知られているので
はおおよそボタンの中心と一致することが知られているので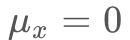 となります。タップ座標はX軸方向に正規分布するはずなので、タップ座標がボタンの範囲に入る確率、つまり成功率
となります。タップ座標はX軸方向に正規分布するはずなので、タップ座標がボタンの範囲に入る確率、つまり成功率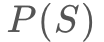 は、
は、
となります。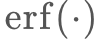 はガウスの誤差関数で、
はガウスの誤差関数で、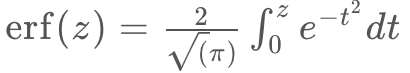 です。
です。
以上でタップ成功率を算出することが可能になりました。まず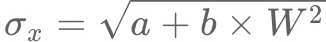 によってボタンの大きさ
によってボタンの大きさ![]() からタップ座標の標準偏差を推定し、これを
からタップ座標の標準偏差を推定し、これを に代入することで、タップ座標が
に代入することで、タップ座標が![]() の範囲に入るかを求められます。
の範囲に入るかを求められます。
ここでは縦長の棒状のボタンについて考え、ボタンのX軸方向の範囲内にタップが入る確率を求めましたが、横長の棒状のボタン(リンクなど)についてY軸方向にタップが入る確率も同じ計算で成功率を求められます。
ではボタンが棒状ではなく円形の場合はどうなるでしょうか。これは、ボタンの範囲を2次元で考えて、二重積分で確率を計算すれば求められます。
棒状のボタンと同様に、X・Y軸方向にどのくらいタップ座標がブレるのかを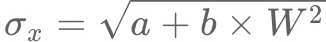 および
および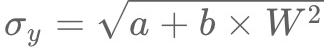 から求め(
から求め(![]() 、
、![]() の値はそれぞれで異なります)、最後に上記の式のように二重積分をします。
の値はそれぞれで異なります)、最後に上記の式のように二重積分をします。
ユーザ実験のデータで検証
大学生・大学院生の合計12名に協力してもらったユーザ実験の結果の一部を紹介します。実験は2日に分けて行い、1日目が横長のボタン、2日目が円形のボタンを使ったものです。下の図のように、スタートボタンをタップしてからターゲットボタンをタップする、という手順を繰り返してもらいます。
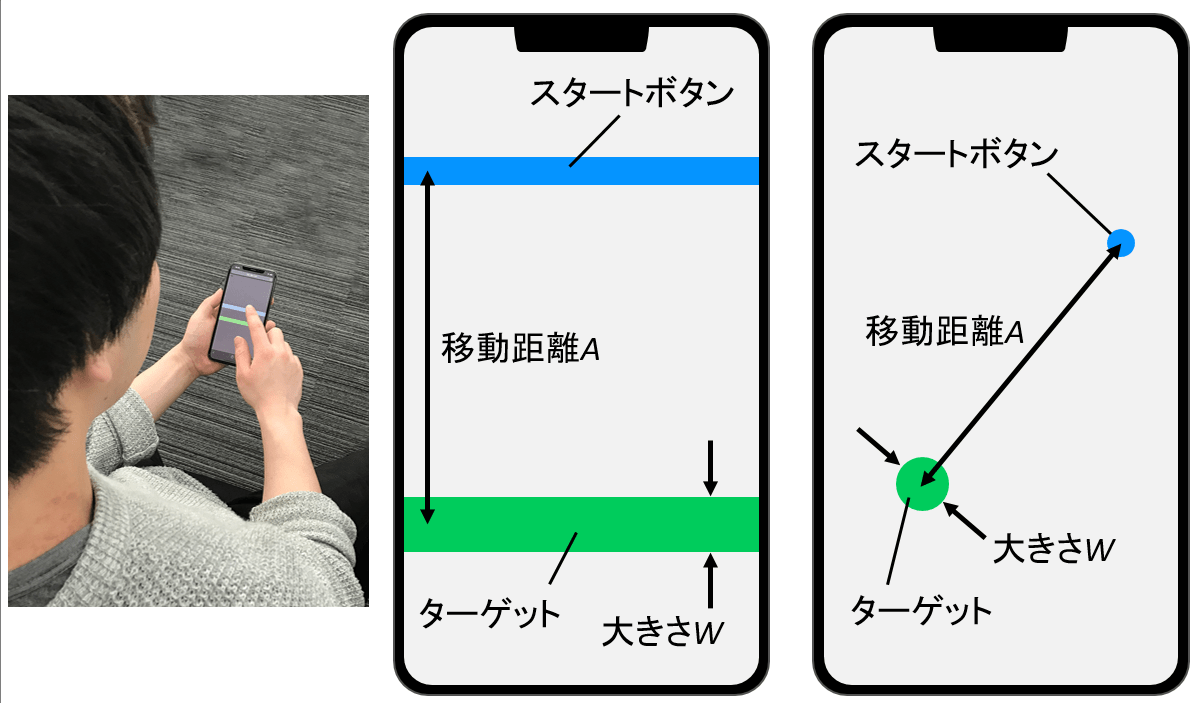
スタートからターゲットまでの距離![]() は4種類、ターゲットの大きさ
は4種類、ターゲットの大きさ![]() は5種類設定しました。
は5種類設定しました。
この合計20種類のターゲット条件がランダムな順序で選出されるのを16回ずつ繰り返しました。
横長の棒状ターゲットの実験結果
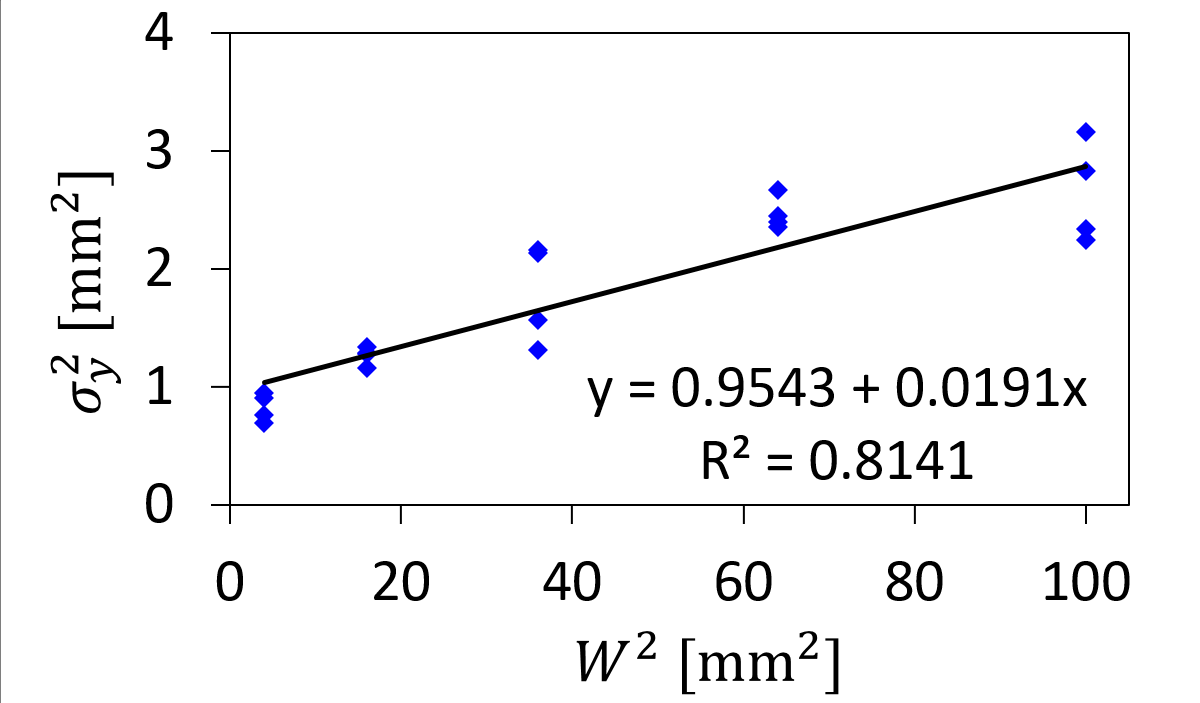
まず「タップ座標のY軸方向のブレ具合は、リンクの大きさに伴って大きくなるはず」という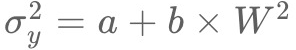 の回帰直線について確認します。すると、回帰式の決定係数が
の回帰直線について確認します。すると、回帰式の決定係数が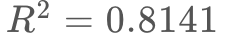 となり、この式がうまく適合していることが分かります。よって、今回の実験では使っていないターゲットの条件(たとえば距離が
となり、この式がうまく適合していることが分かります。よって、今回の実験では使っていないターゲットの条件(たとえば距離が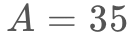 mmで大きさが
mmで大きさが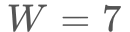 mmなど)であっても、得られた回帰式
mmなど)であっても、得られた回帰式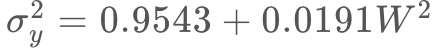 に
に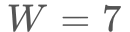 を代入すれば、タップ座標の分散を高精度に推定できるはずです。
を代入すれば、タップ座標の分散を高精度に推定できるはずです。
次に、 を使ってタップの成功率を推定しました。下の図のように、全20種類のターゲット条件で実際に測定したタップ成功率と、今回のモデルで推定した成功率を並べると、実測と推定の成功率が近いことが分かります。実測と推定成功率の相関を見ると
を使ってタップの成功率を推定しました。下の図のように、全20種類のターゲット条件で実際に測定したタップ成功率と、今回のモデルで推定した成功率を並べると、実測と推定の成功率が近いことが分かります。実測と推定成功率の相関を見ると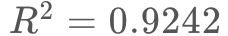 となっており、また平均絶対誤差は3.266%です。
となっており、また平均絶対誤差は3.266%です。
円形ターゲットの実験結果
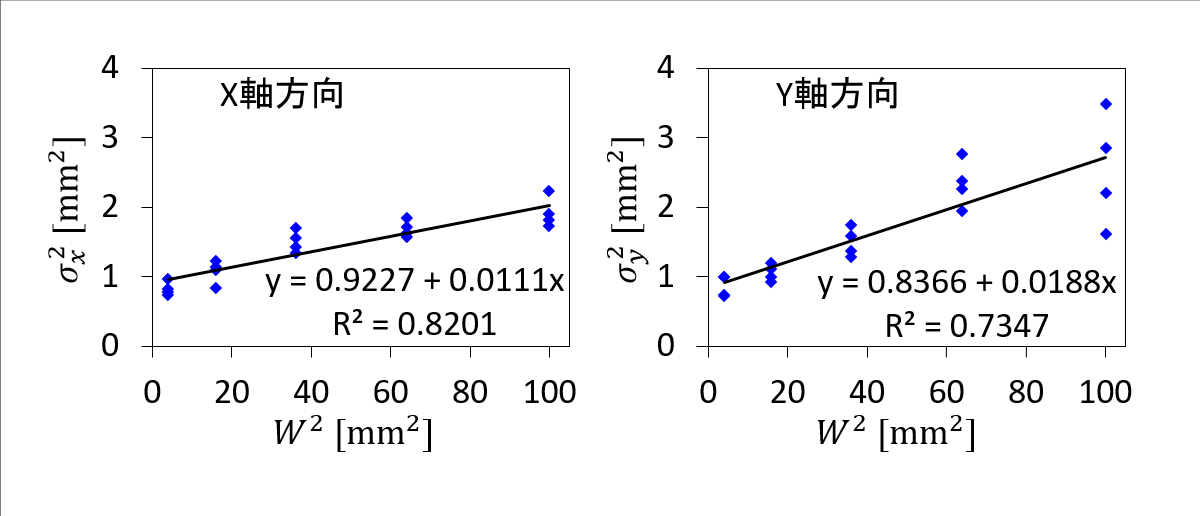
円形ターゲットは、まずX軸とY軸の分散を別々に分析します。その結果は、
となりました(下図)。
次に、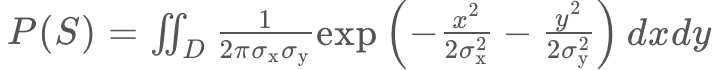 を使ってタップの成功率を推定したのが下の図です。
を使ってタップの成功率を推定したのが下の図です。
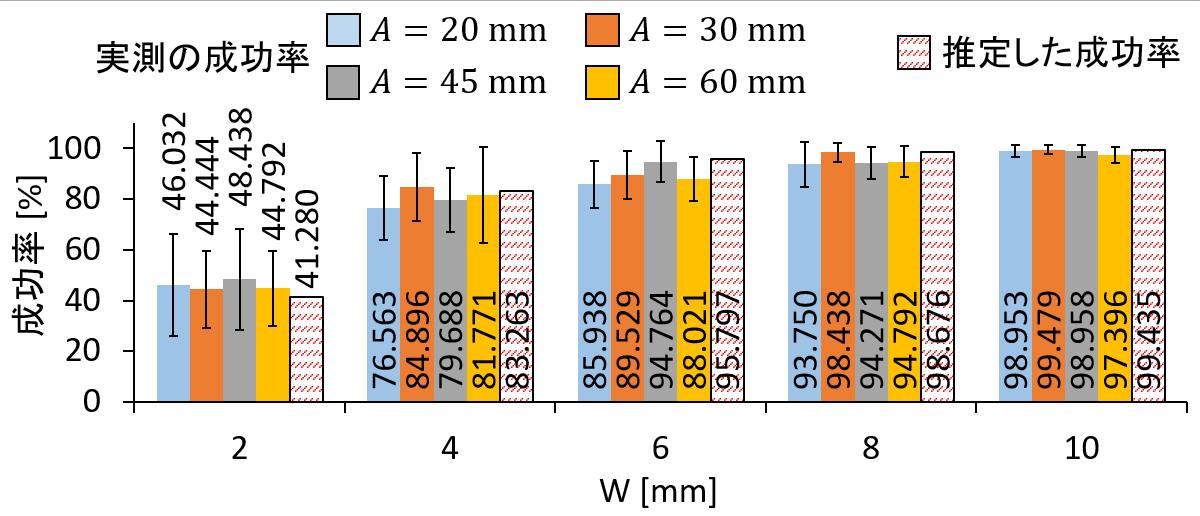
実測と推定成功率の相関を見ると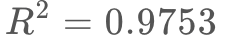 となっており、また平均絶対誤差は3.671%です。
となっており、また平均絶対誤差は3.671%です。
ボタンまでの距離の影響
今回検証した推定モデルでは、タップ成功率はボタンの大きさ![]() のみに依存すると仮定していました。実際にさまざまな研究が、タップ(あるいはマウスカーソルでのクリック)座標の分布は、スタート地点からターゲットまでの距離に影響を受けないことを示しています。しかし一方で、操作スピードが速い場合には、タップ座標の分散
のみに依存すると仮定していました。実際にさまざまな研究が、タップ(あるいはマウスカーソルでのクリック)座標の分布は、スタート地点からターゲットまでの距離に影響を受けないことを示しています。しかし一方で、操作スピードが速い場合には、タップ座標の分散![]() は移動距離
は移動距離![]() の影響を受けるとする研究もあります。
の影響を受けるとする研究もあります。
これはつまり、勢いよくボタンを狙いに行ったときは、その移動距離の分だけスピードに乗っているため、タップ座標のブレも大きくなることを意味しています。今回の実験データでは、ターゲットまでの距離![]() と大きさ
と大きさ![]() はタップ座標の分散
はタップ座標の分散![]() に対して交互作用が認められず、各々が与えた影響は独立でした。よってそれぞれの影響を合算し、
に対して交互作用が認められず、各々が与えた影響は独立でした。よってそれぞれの影響を合算し、
というモデルで分散を推定した場合と比較します。
まず横長の棒状ターゲットについてです。上側が元々のモデル、下側が移動距離![]() を考慮した新しいモデルです。
を考慮した新しいモデルです。

タップ座標の分散の適合度は、補正![]() がわずかに向上していますが、
がわずかに向上していますが、![]() の値を見ると変化はほぼないと言えます(今回の研究では
の値を見ると変化はほぼないと言えます(今回の研究では![]() の差が10以上のときに、意味のある精度向上とみなしています)。そしてタップ成功率について、実測値と推定値の相関がわずかに向上していますが、平均絶対誤差はやや悪化しています。よって、距離
の差が10以上のときに、意味のある精度向上とみなしています)。そしてタップ成功率について、実測値と推定値の相関がわずかに向上していますが、平均絶対誤差はやや悪化しています。よって、距離![]() を考慮することの明確なメリットは確認されませんでした。
を考慮することの明確なメリットは確認されませんでした。
次に円形ターゲットの結果です。まず距離![]() を考慮しないもともとのモデルについて、X・Y軸それぞれの分散の推定結果と、この2つを使った成功率をまとめると、
を考慮しないもともとのモデルについて、X・Y軸それぞれの分散の推定結果と、この2つを使った成功率をまとめると、
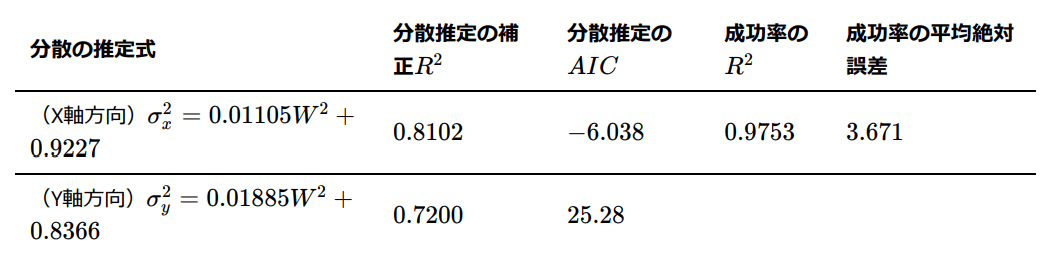
となりました(成功率の結果はX軸の方にまとめて記載しています)。そして距離![]() を考慮したものは、
を考慮したものは、

X・Y軸のそれぞれについて、分散を推定したさいの![]() の差が10未満であり、距離
の差が10未満であり、距離![]() を考慮しても分散の推定精度はあまり改善していません。また成功率の推定精度については、
を考慮しても分散の推定精度はあまり改善していません。また成功率の推定精度については、![]() を考慮すると
を考慮すると![]() および平均絶対誤差が悪化することが分かります。よって円形ボタンに関しては、ターゲットまでの距離
および平均絶対誤差が悪化することが分かります。よって円形ボタンに関しては、ターゲットまでの距離![]() を考慮しない方が良さそうです。
を考慮しない方が良さそうです。
ボタンの大きさとタップ成功率のグラフ
今回の実験で用いたモデルから、ボタンの大きさ![]() とタップ成功率の関係は下図のようになります。
とタップ成功率の関係は下図のようになります。
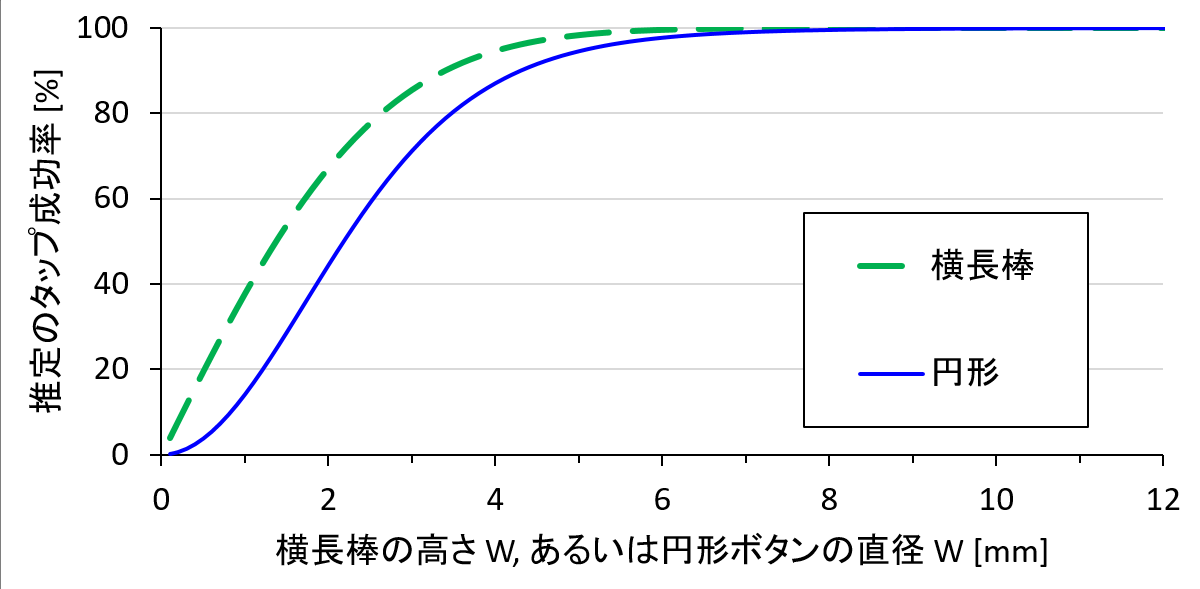
これによると、ボタンの大きさが4 mm程度までは成功率が急激に上昇し、4~6 mm では緩やかにカーブを描き、6 mm以上ではほぼ平坦になっています。たとえば横長の棒状ターゲット(リンクなど)の高さが7 mmのときには成功率は99.91%、8 mmのときには99.98%だと推定されるので、すでに7 mmだけ確保しているのであればリンクをそれ以上大きくするメリットはほとんどありません。一方で、もしリンクの高さが3 mmであれば85.52%、4 mmであれば94.64%になり、ミスタップを9%程度も減らせることになります。同じ1 mmの差でも、タップ成功率の観点ではメリットに大きな差があることが分かります。
このような議論は成功率の推定モデルなしでおこなうのは難しいと考えています。また、ある程度の大きさを確保したボタンであれば、ミスタップの発生率自体が数%程度なので、ミスタップを計測するために何百回もタップして「今回実装したボタンは98.8%の確率でタップが成功したので十分だった」などとレポートするのは時間とコストがかかります。このモデルを使って、UIをデザインする時点で精度良くタップ成功率を推定できれば、デザイナーは他の仕事(見た目のデザインやボタンの配置など)に時間を割くことができるなど、波及的な効果も期待できます。これらが使いやすいアプリやウェブページの提供にもつながり、ユーザの満足度を高めることになると考えています。
おわりに
今回はタップ成功率を推定するモデルの解説をしました。しかしこのモデルが役立つのはUIデザインの一端であり、このモデルを活用することで「このボタンは成功率が低いけれど、使用頻度は低いから他のボタンにスペースを割くべきだ」などと共通の認識を持ってデザインを決定することができるようになると思います。UIデザインは経験に頼る部分も大きいですが、こういった研究がその議論の根拠となるデータを提供できれば幸いです。
なお、この計算を簡単にするためのツール(ウェブブラウザー上で動作するもの)を社内のデザイナー向けに実装しました。リンクやボタンの大きさを入力すると、推定される成功率が表示されます。このような、研究成果を活用してもらうための活動も行っています。今後もUIデザインを良くするための研究やその研究成果を多くの人に使ってもらうための活動を続けていきたいと思います。
参考文献
[1] Yamanaka and Usuba. Rethinking the DualGaussian Distribution Model for Predicting TouchAccuracy in On-Screen-Start Pointing Tasks. PACM HCI, Vol. 4, No. ISS, Article 205, 2020.
[2] Tao, Yuan, Liu, and Qu. Effects of button design characteristics on performance and perceptions of touchscreen use. International Journal of Industrial Ergonomics, Vol. 64, pp. 59-68, 2018.
こちらの記事のご感想を聞かせください。
- 学びがある
- わかりやすい
- 新しい視点
ご感想ありがとうございました