NGT - 最適化グラフの生成方法 -

NGTやNGTの応用として物体認識や類似物体検索の研究開発を行っているYahoo! JAPAN研究所の岩崎です。今回でNGTの解説は最後ですので、グラフ型インデックスの根幹となるグラフの構造に関して詳しく説明します。

グラフの構造と検索性能（速度と精度）との関係

初回では簡便にグラフの生成方法を説明しました。その中で説明したアルゴリズムにより生成されるグラフ（ANNG）では登録初期のノードに多数のエッジが付与されます。また、オブジェクト空間内での登録オブジェクトの分布の偏りにより、特定のノードにエッジが多数付与されるといった状況が容易に発生します。

エッジが多いノードでは検索時に探索するノード数が増えるので、必然的に検索時間が増加します。だからといって、エッジ数を減らすと探索できないオブジェクトが増加し、検索漏れが発生します。したがって、性能向上にはエッジを適切に設定することが極めて重要です。

ANNGではグラフ生成時に無向エッジ（双方向にリンクされているエッジ）でオブジェクトを接続していましたが、1本の無向エッジを出力エッジと入力エッジの2本の有向エッジとして捉え、有向エッジとしてグラフを最適化します。出力エッジは対象ノードから他のノードへたどることができるエッジで、入力エッジは他のノードから対象ノードへたどることができるエッジです。

入力エッジ数が少ないノードは到達でき難くなるので、検索漏れになる可能性があります。検索時において個々のエッジへの到達確率がもし一定だとすると個々のノードの入力エッジ数が1以上の一定数であれば、当確率にすべてのノードに到達できそうです。ただし、入力エッジ数が少ないほど遠回りとなるパスが増えることになるので、結局、到達できなくなる可能性が高まります。つまり、入力エッジ数はノードごとに一定で、かつ、多いほど良いと考えられます。

ただ、入力エッジは接続元のノードにとっては出力エッジです。したがって、入力エッジ数を増やすほど必然的に出力エッジ数が増えるので、個々のノードにおける近傍ノードの探索数が増えて、結果的に検索時間が増加してしまいます。

さらに、グラフ型インデックスの基本条件としてグラフは連結グラフ（任意の2つのノード間のパスが必ず存在するグラフ）である方が望ましいです。なぜなら、探索起点ノードからクエリオブジェクトの近傍ノード（検索されるべきノード）へのパスが存在しなければその近傍ノードに到達できなくなるからです。

これらのことから、

1. 各ノードに同数の入力エッジを付与する
2. グラフの連結性を高める
3. 出力エッジ数の増加による速度低下が発生しない範囲で各ノードの入力エッジ数を増やす

という条件でグラフを生成すれば最適なグラフが生成されます。では、このようにエッジ数をコントロールするにはどうすれば良いかを次に説明します。

入出力エッジ数の調整

簡便のためにk最近傍グラフから最適化されたグラフを生成する方法を説明します。入力エッジ数をn_iとする場合には、k=n_iのk最近傍グラフを用意します。1の対処としては、このk最近傍グラフのすべての有向エッジの向きを逆転すれば容易に入力エッジ数が一定数n_iのグラフが生成できます。

ANNGは連結グラフなのですが、k近傍グラフは連結グラフではありません。連結グラフではないk近傍グラフから生成されるグラフは連結グラフにはならないのですが、2の対処としてk最近傍グラフの元のエッジを一部（n_o本）加える（無向エッジにする）ことで連結性が高まります。

では、ここまでのグラフ生成過程を下図で説明します。

（a）はn_i=3のk最近傍グラフです。（b）は（a）のk最近傍グラフのエッジを反転した入力エッジ数n_i=3のグラフです。（c）は（a）のk最近傍グラフの各ノードの短いものからn_o本のエッジを抽出した出力エッジ数n_o=1のグラフ（k=1のk最近傍グラフ）です。この例では出力エッジとして最短の1本のエッジのみを抽出しています。（b）と（c）のグラフを合成して入力エッジ数と出力エッジ数を調整した（d）のグラフが生成できます。このグラフをONNG（Optimized Nearest Neighbors Graph）と呼んでいます。

では、次に3の対処としてn_i、n_oをどのように決めるかです。まず、期待する精度をあらかじめ決めます。その上で評価関数をその精度における検索時間として、評価関数を最小とするn_i、n_oを探索すればよいです。しかし、検索時間はさまざまな外部要因により安定しないので、評価関数として検索処理時の距離計算の回数を代用します。過去の実験で得られた値の一例ではn_i=120、n_o=10となっており、多数のエッジを有するグラフがONNGとして生成されます。

NGTでの実際のグラフ生成ではANNGから直接ONNGを生成していますが、ANNGから近似k最近傍グラフを生成した上で上記処理を経てONNGを生成していると捉えていただければ良いです。

ショートカットエッジの削減

上記によって各ノードにとって入出力エッジ数が最適化されたグラフが生成できます。次に、検索時のパスを考慮して無駄な出力エッジを減らします。

パスとして無駄なエッジとはショートカットとなるエッジの一部です。ノードN_aからノードN_bへのパスにおいて複数のノードをショートカットできるようなエッジは、ショートカットの効果が高いので削除する必要はないです。しかし、単一ノードのみをショートカットするようなエッジは大量に存在し、単一ノードのみのショートカットの効果よりエッジ数の増加による処理時間の増加の度合いの方が大きいので速度低下をもたらします。そこで単一のノードのみをショートカットするようなエッジを削除します。他にも削除の条件があるのですが詳細はONNGの技術レポート^*1をご参照ください。この削除処理をすべてのノードに対して行います。下図はショートカットエッジの削除の例です。

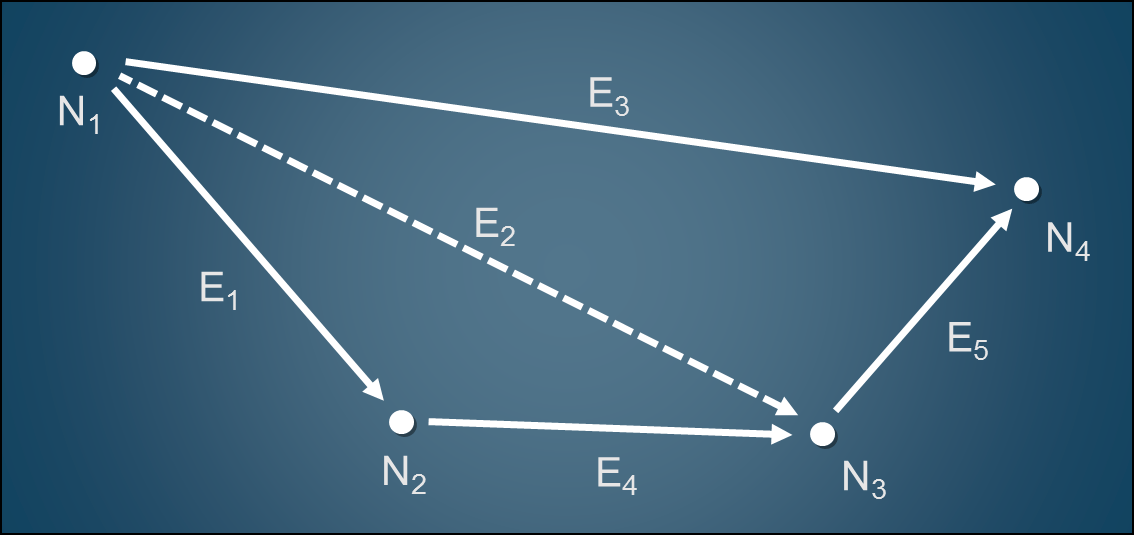
N₁のエッジを試みます。N₁からN₃のパスに着目するとパス｛N₁,N₂,N₃｝が存在しています。E₂はそのパスのショートカットエッジ｛N₁,N₃｝です。E₂はN₂のみしかショートカットできないのでE₂を削除します。次にN₁からN₄のパスに着目するとパス｛N₁,N₂,N₃,N₄｝が存在します。E₃はそのパスのショートカットエッジ｛N₁,N₄｝ですが、N₂とN₃の2つのノードをショートカットできるので削除しません。E₃を削除すると、検索時にN₂とN₃の2つのノードを経由しなければならず、探索コストが増大するからです。

検索時の出力エッジ数の調整

以上により最適化されたグラフ（ONNG）が生成できるのですが、前述のように所望の精度をあらかじめ決めた上で、最適な入出力エッジ数を探索しグラフを生成します。しかし、実際には精度重視または速度重視といったように、各検索要求によって重要視する点が変わる可能性があります。もし、精度が低くくても検索時間が短い方が良いのであれば、検索時にノードごとの参照するエッジ数を実際のエッジ数よりも減らすことで検索時間を短くできます。

参照エッジ数を減らすとは、すなわち出力エッジ数を減らすことと同じです。出力エッジ数を検索時に削減することで低精度に対応することが可能です。したがって、グラフ生成時には高精度が得られるように入出力エッジ数を調整しておくことで、検索時には低精度でも高精度でも常に高速な検索が可能です。こちらも詳細はONNGの技術レポート^*1に記載していますので、ご興味があればご参照ください。

以上で、連載してきましたNGTの技術解説は終わりです。これを読んでグラフ型インデックスに興味を持っていただける人が増えれば幸いです。

*1: Iwasaki, M., Miyazaki, D.: Optimization of Indexing Based on k-Nearest Neighbor Graph for Proximity. arXiv:1810.07355 [cs] (2018). (pdf)

Yahoo! JAPAN研究所　岩崎雅二郎

これまでのNGT解説シリーズ

• グラフ型インデックスによる近似近傍検索の基本
• グラフの探索起点の選択方法
• 検索ロジックの詳細と実装方法
• 最適化グラフの生成方法