TL;DR
量子アニーリングって楽しいよ!!
はじめに
こんにちは、寺田晃太朗 (@kotarot) といいます。Yahoo! JAPANでデータプラットフォームエンジニアとして働いています。今年 (2018年) 4月に新卒で入社しました。Yahoo! JAPAN Tech Advent Calendar 2018の15日目を担当いたします。
本記事では、現在の自分の業務とは直接関係ないテーマですが、自分が最近注目しているテクノロジーという観点から「量子アニーリングってそもそもなに?って話と最近の技術・業界動向」を紹介します。
新しい技術ってなんとなくわくわくしませんか?自分は新しい技術やわくわく感が大好きです。なかでも量子アニーリングは自分がおもしろいと感じていて、現在の主流であるCPU等で動作するノイマン型コンピュータとは違った原理で動くところがおもしろいし、未来のテクノロジーっぽさを感じさせるところがおもしろいし、可能性が未知数なところもおもしろいし、そういったわくわく感を共有したくて今回このテーマを紹介したいと思いました。
本記事はTech Blogということもあり基本的にはソフトウェアエンジニアを対象として書いていますが、そうでない人でもなるべく読みやすいように心がけます。量子アニーリングの「量子」ってワードからどうしても難しさが先行してしまいそうですが、たとえを用いてなるべく直感的に理解しやすいように書いてみました。また後ろの方では、実際のプログラミングの様子も載せてあります。出てくる計算は足し算と掛け算のみです。本記事が少しでも技術解説の助けになりましたら嬉しいです。
量子アニーリングをワカッタ気になろう
猫空間を考えることにしましょう。
ここには不思議な猫がいます。この猫は「白猫」にも「黒猫」にもなれる不思議な猫です。ただし、「白」か「黒」にしかなれず、そのほかの色の猫にはなることはできません。


猫の意思
猫の意思とは、1匹の猫単体に作用する力のことです。
いま、猫が1匹いるとします。
その猫は、自分自身が「白猫になりたいという思い」もしくは「黒猫になりたいという思い」を力として作用させることができます。「白猫になりたいという思い」が作用すればその猫は「白猫」になりますし、「黒猫になりたいという思い」が作用すればその猫は「黒猫」になります。もちろん、どっちの色になっても構わないっていう特に意思を持たない猫がいてもOKです。
この意思の力を「猫単体に作用する力」と呼ぶことにします。


猫の交友関係
猫の交友関係とは、2匹の猫間に相互で作用する力のことです。
いま、猫が2匹いるとします。
2匹の猫の間には、仲が良い関係と仲が悪い関係があります。もちろん、仲が良くも悪くもない無関心な猫同士の関係もありです。仲が良い関係の場合は「お互いに同じ色の猫になりたい力」、仲が悪い関係の場合は「お互いに違う色の猫になりたい力」が作用します。「お互いに同じ色の猫になりたい力」が作用すれば2匹の猫は「白猫と白猫」もしくは「黒猫と黒猫」になりますし、「お互いに違う色の猫になりたい力」が作用すれば2匹の猫は「白猫と黒猫」もしくは「黒猫と白猫」になるでしょう。
これを「猫間の相互に作用する力」と呼ぶことにします。


これらの力を組み合わせてみる
「猫単体に作用する力」と「猫間の相互に作用する力」を組み合わせるとどうなるでしょうか。
いま、猫Aと猫Bの2匹の猫がいるとします。
2つの力を組み合わせて次のような状況を考えます。
- 猫Aには「白猫になりたいという思い」が作用している、
- 猫Bは自分の色には無関心であり「猫単体に作用する力」は作用していない、
- 猫Aと猫Bは仲が悪く「お互いに違う色の猫になりたい力」が作用している。
どうなるでしょうか?
猫Aは「白猫になりたいという思い」のため「白猫」になり、「お互いに違う色の猫になりたい力」により猫Bは「黒猫」になるでしょう。これで2匹ともハッピーです!

では、次の状況ではどうでしょうか。
- 猫Aには「黒猫になりたいという思い」が作用している、
- 猫Bは自分の色には無関心であり「猫単体に作用する力」は作用していない、
- 猫Aと猫Bは仲が良く「お互いに同じ色の猫になりたい力」が作用している。
どうなるでしょうか?
猫Aは「黒猫になりたいという思い」のため「黒猫」になり、「お互いに同じ色の猫になりたい力」により猫Bも「黒猫」になるでしょう。これで2匹ともハッピーです!
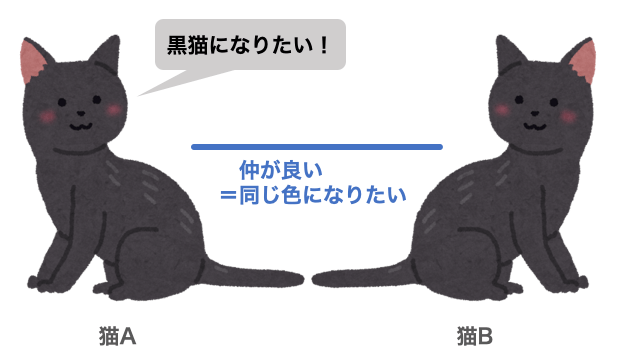
次に、これらの力に「強さ」を導入しようと思います。強さは数値で表すものとします。次のような状況を考えてみます。
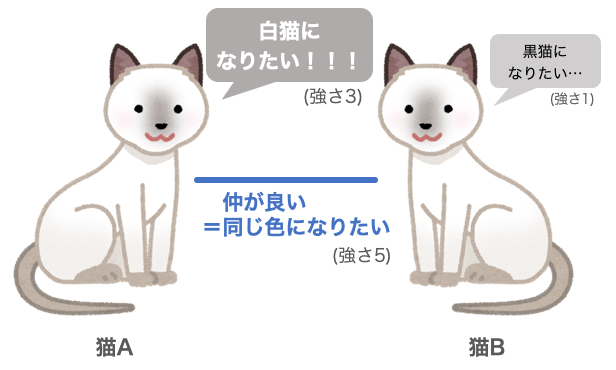
- 猫Aには「白猫になりたいという思い」が「3の強さ」で作用している、
- 猫Bには「黒猫になりたいという思い」が「1の強さ」で作用している、
- 猫Aと猫Bはとても仲が良く「お互いに同じ色の猫になりたい力」が「5の強さ」作用している。
ちょっと複雑になってきました。猫Aは「白猫」になりたがり、猫Bは「黒猫」になりたがり、けれど猫Aと猫Bは仲が良く「同じ色」になりたがっています。矛盾していますね。
しかし、強さに注目すると、3つめの「猫間の相互に作用する力」がなんとなく強そうな上に、猫Aと猫Bのそれぞれのなりたい色の意思は、強さ3である猫Aの意思のほうが強そうなので、なんとなく猫Aが「白猫」で猫Bも「白猫」になりそうな気がします。こうなれば少し妥協しましたが2匹ともまあまあハッピーですね!
定式化
「なんとなく」とか「気がする」とか、ちょっと曖昧すぎました。これまでは直感的な説明をしてきましたが、ここで明確に定義していきたいと思います。これまで直感的に考えてきたことを定式化します。
直前の例で考えます。猫Aと猫Bをそれぞれ sA と sB という2値変数で表します。変数といっても +1 または -1 の2種類しか取れない変数です。猫Aが白猫のとき sA = +1 と表し、黒猫のとき sA = -1 と表すことにします。
猫たちがいる空間の不快指数を定義して数値化します。不快指数をHで表します。不快指数Hが数値的に大きいとき猫空間はアンハッピーであり、数値的に小さいときに猫空間がハッピーで平和であることを表します。不快指数Hを最小にしてみんながハッピーになることがゴールです。
各作用には強さを導入したのでした。それを利用して、この2匹の猫空間の不快指数Hを次のように定義します。
H = - 3×sA + 1×sB - 5×sA×sB
第1項は猫Aに単独で作用する強さ3の力、第2項は猫Bに単独で作用する強さ1の力、第3項は猫Aと猫Bに相互に作用する強さ5の力を表しています。
もちろんみんなハッピーを望んでいます。つまり、不快指数を最小にしたいです。各猫の色がとりうる全パターン調べてみて、猫空間の不快指数がどうなるか調べてみましょう。
| sA | sB | H |
|---|---|---|
| +1 (白猫) | +1 (白猫) | -3+1-5 = -7 (最小!) |
| +1 (白猫) | -1 (黒猫) | -3-1+5 = +4 |
| -1 (黒猫) | +1 (白猫) | +3+1+5 = +9 |
| -1 (黒猫) | -1 (黒猫) | +3-1-5 = -3 |
たしかに、sA=+1、sB=-1、すなわち猫Aが白猫で猫Bが白猫のときに不快指数が最小となって猫空間がハッピーになったことがわかります!
ちなみに、最大のところである sA=-1、sB=+1、すなわち猫Aが黒猫で猫Bが白猫のときを見てみます。猫Aは白猫になりたいのに黒猫になり、猫Bは黒猫になりたいのに白猫になり、猫Aと猫Bは仲が良いのに違う色になってなにもかもが悪いことがわかります。このように、理にかなった定式化ができたことがわかります。
一般化
さて、これを一般化しましょう。
実はこの不思議な猫は「スピン」という名前がつけられていました。そして、不快指数と呼んでいたものは一般的には次のように表現されます。
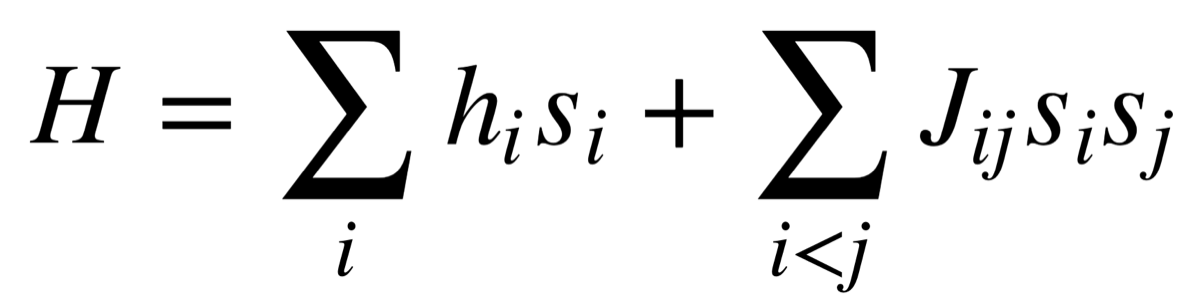
- si はスピンです。+1 or -1 の値を取ります。これはスピンが上向き or 下向きであるとも表現され、白猫と黒猫に相当します。
- hi はスピンsiに「単体に作用する力」の強さのことで「外部磁場係数」といいます。siの向きを上向きに作用させるときはhiの符号をマイナスに設定します。
- Jij はスピンsiとスピンsjの間に「相互に作用する力」の強さのことで「相互作用係数」といいます。siとsjを同じ向きになるように作用させるときはJijの符号をマイナスに設定します。
突如シグマ (総和記号) が出てきましたが、1個目のシグマは「すべてのスピンに対して合計する」を表していて、2個目のシグマは「すべての相互作用しているスピンの組に対して合計する」という計算を表しています。計算している内容は上の猫のたとえで例示したこととまったく同じです。
Hのことをエネルギーといいます。エネルギーが最小であるようなスピン状態のことを安定状態 (もしくは基底状態) といいます。これは猫空間において不快指数が最も小さいときのそれぞれの猫の色の状態と対応しています。
スピンとその接続で構成されたモデルのことを「イジングモデル」といいます。この式を用いることで任意のグラフトポロジ (相互作用のつながり方) をもつイジングモデルのエネルギーを計算できます。これまでの例では数個のスピン (数匹の猫) のイジングモデルを扱いましたが、大量のスピンが複雑に接続されたイジングモデルの基底状態を探索することは、それ自体がとてもハードな問題です。
そして、つまりアニーリングマシンとはなにかというと、「イジングモデル」ならびに「外部磁場係数」と「相互作用係数」を入力したときに、イジングモデルのエネルギーが最小となるようにスピンの状態が変化して、最後、「それぞれのスピンの向き」が出力されるというマシンなのです。
ここまで、物理的な観点からはかなり雑な説明だったと思いますし、実際「量子」という言葉は全く出てきません。けれど、ユーザー視点からみた量子アニーリングマシンってこれがすべてです。
コードで理解しよう
数式での計算は頭が混乱しそうです。本記事を読んでくださっている方はソフトウェアエンジニアの方が多いと思いますので、コードで理解するのが一番の近道でしょう。
リクルートコミュニケーションズが、PyQUBOという量子アニーリングのアプリケーションフレームワーク (Pythonで記述されたアニーリングのためのDSL) を開発しOSSとして公開しています。これを使ってみます。PyQUBOはバックエンドでD-Wave (最先端の量子アニーリングマシンを作っている会社およびそのマシン) のSDKと連携することで本物の量子アニーリングマシンと接続できるとのことですが、それはすぐには実施することができないので今日は単独でこのツールを利用します。単独で利用してもPyQUBO自体にSimulated Annealingが組み込まれていてアニーリングシミュレータとしてちゃんと解を得られるところまで計算できます。
インストール
pipでインストールできます。
pip install pyquboPythonスクリプトのライブラリのインポート部分は次の行のように書けます。
from pyqubo import Spin, solve_ising例1: 猫の意思
# 【例1】猫の意思
# - 猫が1匹「白猫 (+1) になりたい」
sa = Spin("sa")
H = -3 * sa # <- sa が +1 になるように強制しています。計算するまでもなく sa=1 のときに H が最小になりますね!
linear, quad, offset = H.compile().to_ising()
solution = solve_ising(linear, quad)
print(solution)以下が出力です。
{'sa': 1} # 猫Aは白猫sA = +1、すなわち猫Aが白猫、となっていることが確かに確認できます。
例2: 猫の交友関係
# 【例2】猫の交友関係
# - 猫が2匹「仲が良いので同じ色になりたい」
sa, sb = Spin("sa"), Spin("sb")
H = -3 * sa * sb # <- sa と sb が同じ向きになるように作用しています。sa と sb が同じ符号のとき H が最小になりますね!
linear, quad, offset = H.compile().to_ising()
solution = solve_ising(linear, quad)
print(solution)以下が出力です。
{'sa': 1, 'sb': 1} # 猫Aは白猫、猫Bも白猫or
{'sa': -1, 'sb': -1} # 猫Aは黒猫、猫Bも黒猫sA=sB=+1 もしくは sA=sB=-1、すなわち猫Aと猫Bは両方とも白猫か両方とも黒猫、となっていることが確かに確認できます。
例3: これらの力を組み合わせてみる
# 【例3】これらの力を組み合わせてみる
# - 猫Aには「白猫になりたいという思い」が「3の強さ」で作用している、
# - 猫Bには「黒猫になりたいという思い」が「1の強さ」で作用している、
# - 猫Aと猫Bはとても仲が良く「お互いに同じ色の猫になりたい力」が「5の強さ」作用している。
sa, sb = Spin("sa"), Spin("sb")
H = -3 * sa + 1 * sb - 5 * sa * sb # <- さっきの式です!
linear, quad, offset = H.compile().to_ising()
solution = solve_ising(linear, quad)
print(solution)以下が出力です。
{'sa': 1, 'sb': 1} # 猫Aは白猫、猫Bも白猫先程、表を使って調べたときと同様に、sA=sB=+1、すなわち猫Aと猫Bは両方とも白猫、となることが確かに確認できます。
で、結局アニーリングマシンを使うと何が嬉しいの?
難しい問題 (組合せ最適化問題とか) が効率的に解けるとされています。実例を次に紹介します。
実際に問題を解いてみよう
やっと問題らしい問題を量子アニーリングで解いてみます。
あなたは、ホテルの支配人です。下の表のように予約が入っています。小さなホテルで部屋数が限られているため最大3部屋しか用意できません。予約したすべてのお客様が宿泊することは可能でしょうか?可能な場合は割り当て方法を考えてください。
| 名前 | 滞在日 |
|---|---|
| Alice | 12/1 ~ 12/5 |
| Bob | 12/1 ~ 12/2 |
| Carol | 12/1 ~ 12/4 |
| Dave | 12/3 ~ 12/6 |
| Ellen | 12/5 ~ 12/7 |
| Frank | 12/7 ~ 12/8 |
この例は規模が小さく、ちょっと頭で考えてれば答えがわかってしまうかもしれません。けれど、巨大なホテルだとしたら頭で考えるのが難しそうです。とにかくこの問題例をアニーリングマシンで解いてみることにします。
問題を量子アニーリングマシンで解くときは基本的に次のような流れに沿って解きます。
(1) 問題の抽出(2) 量子アニーリングマシン (イジングモデル) へのマッピング(3) アニーリングの実行(4) 解の解釈
(1) 問題の抽出
まずは、対象の問題を量子アニーリングで解くことのできるようにできる限りシンプルな問題に切り出すことが必要です。
この問題は実はグラフ頂点彩色問題に帰着させることができます。
グラフ頂点彩色問題とは、任意のグラフ G=(V,E) と色総数 K が与えられたとき、すべての頂点を、隣接する頂点 (すなわち、辺で接続されている頂点) が同色にならないという制約下でK色に塗り分ける (彩色する) ことができるか?それはどのような塗り方か?を見つける問題です。計算複雑性クラスではNP完全であり、多項式時間で解くことができない問題とされています。つまり簡単に言うと普通に解くのは結構ハードな問題とされています。
今回の問題では、各予約をグラフの頂点とします。宿泊日が重なる予約同士を辺でつないでグラフを完成させます。宿泊日が重なっているということは同じ部屋に割り当てることができないということなので、このグラフに対して頂点彩色問題を解けば彩色の結果がそのまま部屋の割り当て結果となるわけです。
予約を上から0始まりで番号を振り、そのようなルールでグラフを構築すると次の図のようなグラフができます。
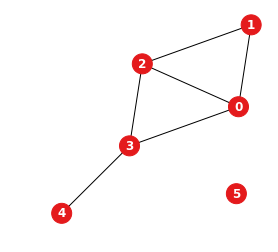
量子アニーリングマシンでは、この抽出したグラフ頂点彩色問題を解けばよいことになります。
(2) 量子アニーリングマシン (イジングモデル) へのマッピング
グラフ頂点彩色問題を量子アニーリングマシンで解いてみましょう。解くためにはイジングモデルの式に落とし込まないといけません。これを最適化問題のイジングモデルへのマッピングといいます。このステップが量子アニーリングでの「プログラミング」に相当します。マッピングにはいくつかの知見やコツが存在します。
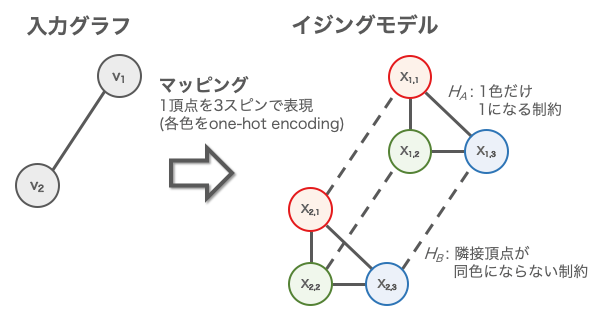
まず、入力のグラフとイジングモデルを対応づけます。今回は入力グラフの6個の頂点それぞれを色数である3個の変数に対応させます。つまり、合計で 6×3 = 18個のバイナリ変数 (=スピン) を用意します。変数xは 0 と 1 の2値を取るもので2次元配列のようなものです。x[i,k]=1 であるとき頂点iが色kに彩色されたことを表現します。要するに、頂点の色を one-hot encoding で表現したことになります。
なお、先程のイジングモデルのエネルギー式では +1 と -1 の2値を取るスピン変数を導入しましたが、このバイナリ変数とスピン変数は互いに変換可能であるため、実際にHを構築するときにはどちらを導入しても問題ありません。PyQUBOはこの違いもいい感じに吸収してくれるので、考えやすいほうを用いれば大丈夫です。
最適解となるときにHが最小となるようにうまく係数を設定することが、マッピングで達成したいことです。
今回は「頂点iが1色のみで彩色される制約」と「隣接頂点は異色で塗り分けられるという制約」をどちらも満たすことを考える必要があります。それぞれをエネルギー式の HA と HB で表現して、目的のエネルギー式Hを構築する方針でいきます。
HA は「頂点iが1色のみで彩色される制約」を表しています。例えば、頂点i=0に注目すると、変数は x[0,0], x[0,1], x[0,2] の3つが関係しています。頂点が1色に彩色されるということは、この3つの変数のうちで1個だけが1で残りすべてが0であるということが常に成り立たなければなりません。そこで3個の変数の値をすべて足し合わせたものを1から引いて2乗することで、ただ1つの変数が1のときにエネルギーが0となりかつ最小となります。このようにして、制約をエネルギー式で表現することができ、HA が導き出されます。
HB は「隣接頂点は異色で塗り分けられるという制約」を表しています。例えば、頂点1と頂点2は隣接しています。そこで、x[1,0]とx[2,0]、x[1,1]とx[2,1]、x[1,1]とx[2,1] は (1, 1) の組合せになってはなりません。隣接頂点が同色に彩色されていることになってしまうからです。x[i,k]とx[j,k]を掛けることで (1, 1) の組合せのときにのみエネルギーが増加することを表現できます。すべて制約を満たすときにエネルギーが0となりかつ最小となることがわかります。このようにして、HB も導き出されます。
まとめると、エネルギーの式は以下の通りです。
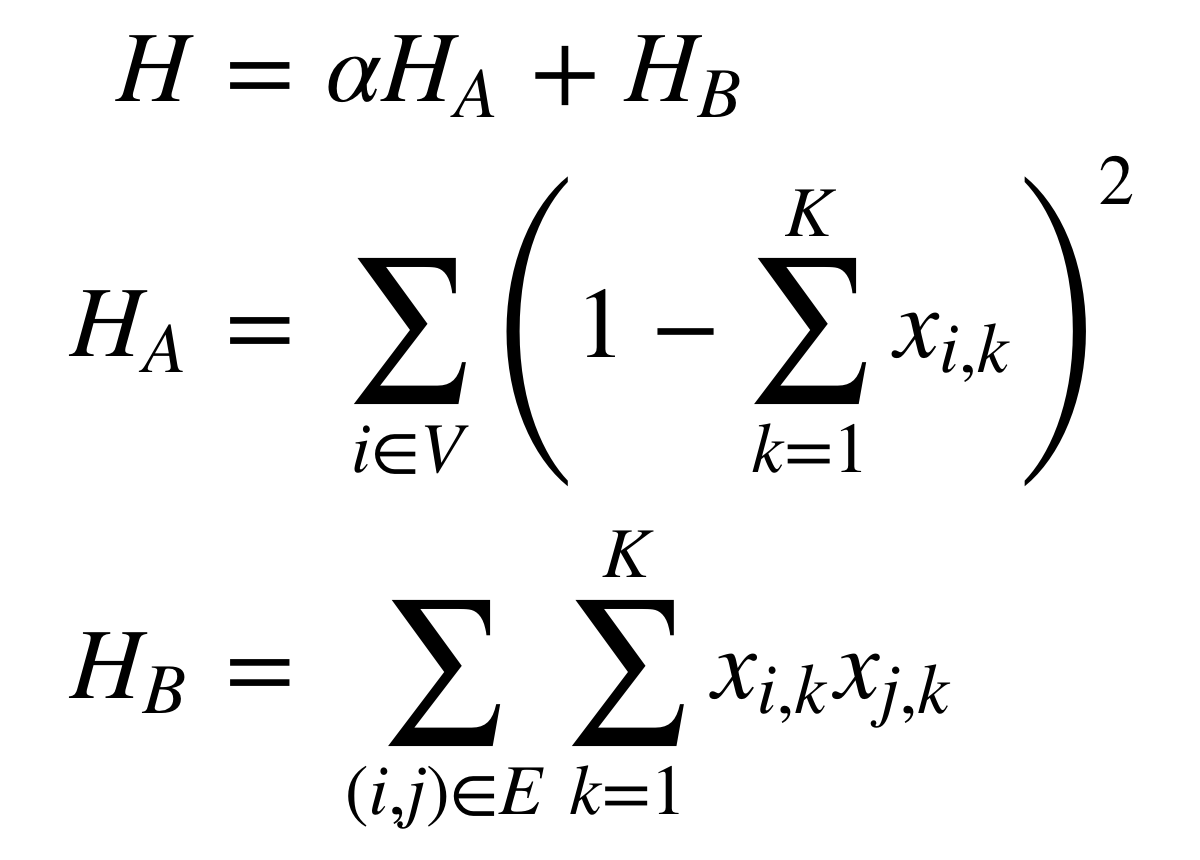
エネルギー式Hは HA と HB を足し合わせればOKです。それぞれのエネルギーの重みを調整するために alpha のような重みパラメータを導入することが多いです (ちなみに今回は alpha=1 としたのであまり関係ないです)。すべての制約を満たすときに、H=0 となります。
グラフ頂点彩色問題は例えばフィックスターズのページでもマッピングの方法がたくさんの図とともに書かれています。よければ一緒に参照してみてください。
これをPyQUBOを用いてプログラミングしたコードを見てみましょう。このコードを記述したJupyter Notebookを同時に参照するとよりわかりやすいと思います。
from pyqubo import Array, Constraint, Sum, Placeholder, solve_qubo
# 頂点数と色数
N = 6
K = 3
# エッジが以下のように与えられる
E = {(0, 1), (0, 2), (0, 3), (1, 2), (2, 3), (3, 4)}下の図は彩色前のグラフです (再掲)。

# 6×3のバイナリベクトルを用意
x = Array.create('x', (N, K), 'BINARY')
# ある頂点iが1色のみである制約
onecolor_const = 0.0
for i in range(N):
onecolor_const += Constraint((Sum(0, K, lambda j: x[i, j]) - 1)**2, label="onecolor{}".format(i))
# 隣接頂点は異色で塗り分けられるという制約
adjacent_const = 0.0
for (i, j) in E:
for k in range(K):
adjacent_const += Constraint(x[i, k] * x[j, k], label="adjacent({},{})".format(i, j))
# エネルギー (ハミルトニアン) を構築
alpha = Placeholder("alpha")
H = alpha * onecolor_const + adjacent_const
# モデルをコンパイル
model = H.compile()
# QUBOを作成
feed_dict = {'alpha': 1.0}
qubo, offset = model.to_qubo(feed_dict=feed_dict)(3) アニーリングの実行
PyQUBOでは内蔵のシミュレータ (Simulated Annealing) で計算できます。今回は省略していますが、(2) で構築したエネルギー式内のパラメータを探索したり、実際に量子アニーリングマシン等のハードウェアを使う場合にはハードウェア上のパラメータを調整・探索する必要があります。
# 最適解を求める
solution = solve_qubo(qubo)
decoded_solution, broken, energy = model.decode_solution(solution, vartype="BINARY", feed_dict=feed_dict)
print("number of broken constarint = {}".format(len(broken)))
# 各頂点の色を取得する
colors = [0 for i in range(N)]
for i in range(N):
for k in range(K):
if decoded_solution['x'][i][k] == 1:
colors[i] = k
break(4) 解の解釈
グラフ頂点彩色後の結果です。各頂点に対応するスピンから +1 となった色を取得して表示しました。
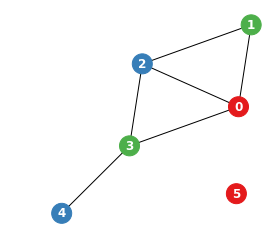
各頂点はただ1色に無事彩色され、隣接する頂点は同じ色にはなっていないことが確認できます。そして、元の問題に振り返ってみると、3部屋で宿泊を受け入れることは可能かという問題に対する答えはYesであり、その部屋の割り当て方法は彩色後の図のようにすればよいことがわかります。
今回はグラフ彩色問題の制約を満たすことだけを考えましたが、これに加えて「部屋数 (色数) を最小にする割り当て方法を見つける」(ちなみにこれはNP困難です) とか「ある予約には特定の部屋を必ず割り当てる」とかの条件を加えてみてもおもしろいかもしれません。エネルギー式の構築方法が変わります。ぜひ考えてみてください。
で、量子アニーリングって実用的に使えるの?
たしかにグラフ彩色問題に対して答えを求めることができました。そして最近は「量子アニーリングは画期的な技術だ」って紹介されることも多いです。確かにおもしろい技術だとは思うのですが、実用上は課題だらけで、まだまだ画期的な技術というには早いような気がします。
いくつかの課題感をまとめます。
ユーザー視点から見ると現状の量子アニーリングはおもちゃレベルであることは否めない
なぜなら現状で量子アニーリングで解ける問題は基本的にCPUで解けてしまうものがほとんどだからです。量子アニーリングでないと解けない、っていうキラーアプリケーションは (私の知る限り) 今のところ存在しません。CPU等でも解ける問題でも、量子アニーリングのほうが効率 (エネルギー効率だったり計算時間効率だったり) が良さそうな問題も見つかっている、といった段階です。
アニーリングマシンで得られる解の「良さ」はわからない
今回取り上げた例題は比較的小さい問題であったため、PyQUBOでベストな最適解 (厳密解) を求めることができましたが、一般にアニーリングマシンは厳密解を得られるわけではありません。アニーリングマシンは探索できた中でエネルギー式の計算結果が最も低いときのスピン状態を解としますので、その出力が厳密解であるか、またはどのくらい「良い」解であるのかはわかりません。
ビット数 (スピン数) の問題
D-Waveの最新のプロセッサをもってしても2048ビット (スピン) しかありません。現実で解きたい問題規模に対して圧倒的にハードウェアリソースが足りない現状です。まともに問題を解くのならば感覚的に最低限でもミリオンオーダーのビット数がないと不十分なのではないかと個人的には考えています。
イジングモデルへのマッピングの問題
そもそもさまざまな問題をイジングモデルにまだ効率的にマッピングできていないという課題もあるかと思います。
まず、NP完全問題に関しては、理論的には任意のNP完全の問題は多項式時間で3-SATに帰着できます。3-SATはアニーリングマシンに載せる方法が存在するため理論的にはどんなNP完全の問題もアニーリングマシンにマッピング可能です。しかし、それではスピンが何個必要になるかわからないし非効率となってしまうことがすぐに想像できてしまいます。
また、より現実的で複雑な問題を考えると、他の問題に帰着という考え方も難しく、問題ごとに個別でイジングモデルへのマッピングを考えるという必要はこれからも避けられない問題として残ると思います。PyQUBOのようなDSLはマッピングのかなりの助けにはなることが期待されますが、まだ汎用なものではないです。
イジングモデルの埋め込みの問題
無事にイジングモデルへマッピングができたとしてもアニーリングマシンのハードウェアで解くためにはさらにハードルがあります。
今回はアニーリングでシミュレータを用いたので隠蔽されていましたが、実際のマシンではハードウェア上の制約があります。というのも、マシン上のイジングモデルのトポロジはマシン特有の形状をしたものであることがほとんどです。一方、問題をマッピングしたイジングモデルは任意のトポロジですので、これをハードウェア上に実装するためにはイジングモデルの変換をする必要があります。また、マシンの外部磁場係数と相互作用係数も必ずしも任意の値を取れるわけではないという係数の解像度の問題もあります。最適化問題のイジングモデルをマシン上のイジングモデルに変換する (これを埋め込みといいます) もまた最適化問題なのです。そのため、効率的な埋め込みアルゴリズムがアプリケーションレイヤーでも必須となっている現状です。埋め込みアルゴリズムだけに特化した問題がAtCoderのプログラミングコンテストの題材となったこともあるくらいです。さらに、たとえマシンに埋め込みができたとしても、アニーリング実行後の物理的なスピン値を元々のイジングモデルのスピン値としてどう解釈するかというアルゴリズムも実用上では必須な課題となっています。
たくさんの人が量子アニーリングが革新的で実用的な技術になることを可能性を信じて、これらの課題 (他にもたくさん) を解決するべく研究・開発が進められています。とてもわくわくします。
ここで、量子アニーリングのアプリケーション応用の動向をいくつか紹介します。
代表的な組合せ最適化問題として知られているKarpの21のNP完全問題をイジングモデルにマッピングした論文が存在しますが、実マシンを使って本当に現実的に許容できる解が得られるのかとか、どのくらいの問題規模まで何かしらの解を得ることができるのかとかは検証がまだまだ必要な段階です。比較的単純な最適化問題の他には、アプリケーションを開発するユーザー企業 (PyQUBOを開発しているリクルートコミュニケーションズ等をはじめとしたような) や大学が多様な最適化問題に取り組んで日々研究を進めています。最近は渋滞の解消など交通流の最適化に用いられるケースが目立ち、機械学習のアルゴリズムにも応用が試みられています。他にも、例えば矩形パッキング問題 (任意の数のあらゆるサイズの矩形が与えられたとき平面上に最も小面積で詰め込む方法を見つける問題) をアニーリングマシンで解くといった比較的複雑なアプリケーションへの応用も試みられていたり等、試行が重ねられている段階です。東北大学のT-QARDのブログでは、量子アニーリングの最新のアプリケーション応用例をタイムリーに紹介しています。
IPAの未踏事業というプロジェクトがあります。そのなかでちょうど今年の10月にアニーリングマシンを対象としたプロジェクトの公募結果が発表されました。若い人材を育成する目的で独創的なアイデアを支援するという目的のプロジェクトとのことで、採択されているテーマが面白そうなのばかり並んでいるのが印象的です。ますます量子アニーリングのアプリケーションの応用研究が進むのではないかと盛り上がっている真っ最中です。
日本でも量子アニーリングマシンを開発するプロジェクトが走っています。大学と民間企業も密接に連携しながらアプリケーションとハードウェアの両面から目まぐるしく研究・開発が進められています。
本物の量子アニーリングマシンを使いたい
チョットワカルと言い張るためにはやっぱり本物の量子アニーリングマシンを触ってみたくないですか? D-WaveがLEAPという量子アニーリングマシンをクラウドでなんと無料で利用できるサービスを今年の10月にリリースして話題になりました。しかし、残念ながら日本からは使うことができません。現在、カナダ・アメリカからしか使えないようです。いろいろとトライアル段階のようです。
量子じゃないアニーリングマシンもあるよ!
ここまで「量子アニーリング」を強調して技術紹介してきましたが、実は量子アニーリング以外にも各種アニーリングマシンが提案・開発されています。日本の企業・研究機関発のマシンで例を挙げると、日立製作所のCMOSアニーリングマシン、富士通のデジタルアニーラ等、既存のCMOSテクノロジーやFPGAを利用したアニーリングマシンが挙げれられます。CMOSアニーリングマシンは今年の9月にリリースされたAnnealing Cloud Webというサービスで実際にウェブ上で動作させることができるようになりました。Web APIも開発中で公開予定とのことです。ますます活用のチャンスは増えるのではないかと思っています。また、さくらインターネットがCMOSアニーリングマシンの評価を始めるというプレスリリースを今年の10月に出しています。
これらNon量子なアニーリングマシンも量子アニーリングマシンと中身の動作原理は違えど本質的にやっているアニーリングは同じです。「量子」というワードのすごそう感やキャッチーさからややイメージが先行しがちな量子アニーリングですが、実際にアプリケーションの開発者・利用者の視点から見たら内部の実装がどうなっているか (量子なのか量子じゃないのか) はあまり関係なく、このあたりをすべてひっくるめて「アニーリングマシン」(もっとかっこいい呼称があればそちらでもよいけど) って呼んでいくほうが今後は自然なのかもしれませんね。
今年もあと半月で終わってしまいますが、こうやって技術や業界の動向を振り返ってみるとハードウェアの開発側もアプリケーションを開発するユーザーもますます増えてきて量子アニーリングあるいはアニーリングマシンが注目されている2018年であることがわかります。様々な人たちがアニーリングマシンの技術にブレークスルーがあると信じて研究・開発に取り組んでいます。身近なところで動作するチップからデータセンターまで、アニーリングマシンが動くようになる時代は遠い未来ではないのかもしれませんね。
おわりに
量子アニーリングとはなにか?というところから、最近の技術動向までを簡単に紹介しました。実用化への道のりはまだ課題が多く容易ではないと思っていますが、おもしろい技術でありいろいろなところで注目され始めている技術であることは間違いなさそうです。
この記事を読んで量子アニーリングの基礎を知った上で、まだ世界で誰も量子アニーリングで解いたことない問題に挑戦してみてください。それが達成できたころには「量子アニーリングがチョットワカル」ようになっているはずです。
私もこの分野は日々勉強中です。みんなで盛り上げていきましょう!社内の方でも社外の方でも、内容に興味をもってくれた方、続きをもっとディスカッションしたい方などぜひ私に声をかけてください!
この度は Tech Blog Advent Calendar でこの記事を書く機会を与えてくださった関係者には大変感謝します。ありがとうございます。最後まで読んでくださった方にも本当に感謝です。ありがとうございました。一緒に未来のテクノロジーを創造していきましょう!
明日の記事もお楽しみに!!
猫の画像: いらすとや
関連記事
- ヤフーCTO藤門、Advent Calendar 「Best Author」に肉ランチで表彰!
(2019年3月28日 linotice)
こちらの記事のご感想を聞かせください。
- 学びがある
- わかりやすい
- 新しい視点
ご感想ありがとうございました



