NGT -グラフ型インデックスによる近似近傍検索の基本-

高次元ベクトルデータの近傍検索（NGT）の研究開発を行っているYahoo! JAPAN研究所の岩崎です。私は応用面では類似画像検索や特定物体認識の研究開発を行っていますが、NGTは画像系だけでなく多種多様なデータ検索に利用できるので多くの方に利用していただきたく、NGTをOSSとして公開しています。

NGTは複数種類のグラフ型インデックスを提供していますが、最近新たにONNG(Optimized Nearest Neighbors Graph)というインデックスを追加しました。これを機会にグラフ型インデックスについて解説しようと思います。

近傍検索のインデックスとは

近傍検索とは、距離関数が規定されたベクトル空間においてクエリとして指定されたオブジェクト（ベクトルデータ）に対して近傍のオブジェクトを取得する検索のことです。近傍検索には範囲検索、最近傍検索、k最近傍検索といった種類がありますが、ここではクエリに対してk個の近傍オブジェクトを取得するk最近傍検索を対象として説明します。

最近では近傍検索といえば近似近傍検索（検索されるべきオブジェクトが検索されない検索漏れが発生する近傍検索）が主流ですが、昔は漏れのない近傍検索のためのインデキシングの研究が盛んに行われていました。しかし、オブジェクトのベクトル空間が高次元になるほど、インデキシングの効果がなくなりほぼ線形探索に近くなってしまうということが認識され、多少の漏れがあっても高速なら良しとする近似近傍検索が主流になりました。近似といってもほぼ漏れのない精度を出すこともできます。ただし、漏れがないことを保証できないという点で近似近傍検索に分類されます。なお、一般に検索精度はパラメータによってコントロールができますが、検索精度を上げると検索時間が長くなり、検索精度と検索時間はトレードオフの関係にあります。したがって、検索精度が同じであれば、検索時間が短い、または、検索時間が同じであれば、検索精度が高い、インデキシング手法が優れていることになります。ここでは検索精度と検索時間をまとめて「検索性能」と表現します。

漏れのない近傍検索ではツリー型のインデックスが主流でしたが、近似近傍検索になるとインデックスの種類が増えていきました。ハッシュ系や量子化系、そして、グラフ型です。それぞれさまざまな改良手法があるので、すべてに当てはまる訳ではないですが、ハッシュ系、量子化系の手法は基本的に検索時にオブジェクトを必要としません。その分高速であったりメモリ使用量が少なかったりするのですが、検索精度を上げにくい傾向があると言えます。グラフ型では検索性能が高い一方で、任意のオブジェクトを検索時に利用することからメモリ上にすべての検索対象のオブジェクトを配置する必要があり、メモリ使用量が比較的多くなります。さらに、グラフ生成のコストが比較的高いという問題点もあります。しかし、前者については、オブジェクトをメモリではなく高速化が進むSSDに載せれば良いですし、後者については、マルチコアで処理すれば良いので、どちらも実用上は問題にならないでしょう。

グラフによる近傍検索

まずは、グラフを用いてどのように近傍検索を実現するかを説明します。グラフはノードと、ノードを接続するエッジで構成されます。インデックスとしてのグラフでは、ノードは検索対象のオブジェクトとなります。また、これらのノードは距離が定義された空間上において近傍のノードにエッジで接続されていなければなりません。簡便なグラフであるk最近傍グラフはその代表例です。k最近傍グラフでは各ノードは近い順にk個の近傍のノードに有向エッジ（エッジの向きが存在する単方向エッジ）で接続されています。

では、最も単純な方法でk最近傍検索の流れを説明します。k最近傍検索ではクエリオブジェクトQと検索結果として返す近傍ノードの個数kが与えられます。検索処理の開始時点ではQを中心とする検索半径rの探索範囲においてrを無限大として初期化します。グラフ上の任意のノードN_seedを探索起点として選択します。ここから最良優先探索を行います。探索起点N_seedからエッジで接続されているすべての近傍ノードをN_nとQの距離を計算します。これらの関係を以下の図に示します。

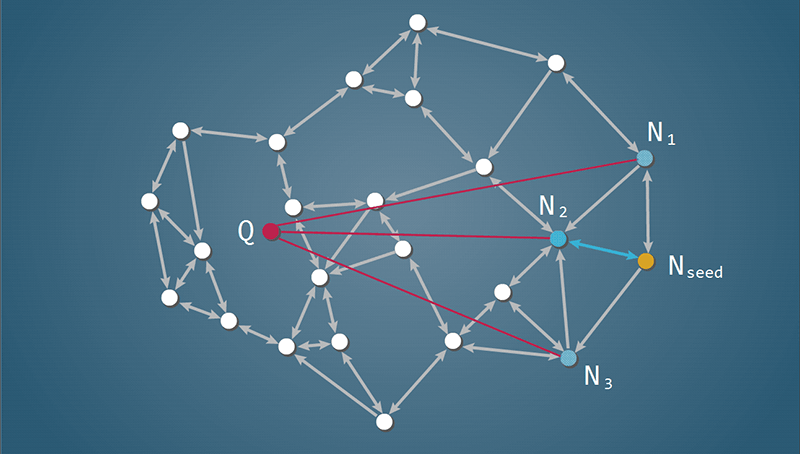
次に、これらの近傍ノードN_nを距離の近い順に並んだ長さkの検索結果リスト（検索結果の候補ノードのリスト）に追加します。そして、N_nの中で最も距離の近いノードへ移動します。この繰り返しです。

では、どうなったら終わるのでしょうか？　グラフにはループになっている経路が存在するので、永遠と巡回してしまいます。そこで、たどったノードにはフラグを立てて、再度たどり着いた時には無視するようにします。また、初期化時にはrは無限大になっていますが、検索結果リストのノード数がkに達したら、そのk番目のノードの距離r_k以上の距離のノードは検索結果になり得ません。したがって、rをr_kに狭めることができます。つまり、探索が進むにつれて検索範囲は狭まっていくことになり、その探索範囲内に探索していないノードがなくなった時が検索の終了となります。なお、ここでは流れをつかんで頂くために多少簡略化して説明しています。kが3の場合の検索の流れを以下の図で示します。

グラフの生成

このような検索方法で高速な検索を実現可能なのですが、事前にk最近傍グラフを作成しなければなりません。k最近傍グラフを作成するためには各ノードに対してk個の近傍ノードを見つけなければならないので、k最近傍検索を行わなくてはなりません。つまり、k最近傍検索を高速に行うためのインデックスを生成するためにk最近傍検索が必要になるという皮肉な状態になります。オブジェクト数が多くなると、全オブジェクト間の距離を計算することでk最近傍検索を行ってk最近傍グラフを構築することは現実的ではありません。

では、どうするかというと、グラフへランダムに1オブジェクトずつ追加していきます。追加する時にk最近傍検索を行わなければなりませんが、生成途中のグラフを用いてk最近傍検索を行います。検索されたk個の近傍のノードと追加するオブジェクトをエッジで接続します。この繰り返しです。グラフを用いるのでk個の近傍ノードを高速に検索できます。その結果、グラフの生成が高速に行えます。kが3の場合のグラフ生成の様子を以下の図で示します。

なお、有向エッジで接続されるk最近傍グラフは連結性が保証されません。つまり、2つ以上の分離したグラフが生成されてしまう場合があり、任意のノードから任意のノードへエッジをたどって行くことができない状態になります。このようなグラフでは当然検索漏れが多くなってしまいます。インデックスとして利用する場合には連結性が保証されるグラフ（連結グラフ）が有利になります。そこで、1オブジェクトをグラフに追加する時には連結性を保証するために無向（双方向）エッジで結合します。このように無向エッジで生成されたグラフはインデックスとして有利ですが、各ノードはk個以上のノードと接続されるので、k最近傍グラフではなくなります。なお、この登録手法を含めグラフ型インデックスに関して特許権をヤフー株式会社が各種取得していますが、NGTを使う限り権利を開放していますので、NGTを商用にも自由に利用できます。

以上が、グラフ型インデックスの簡単な説明でした。これでも十分高速なのですが、さらに検索性能を向上するにはどうするかといったことを次回説明したいと思います。

Yahoo! JAPAN研究所　岩崎雅二郎