はじめに
はじめまして、安藤義裕と申します。ヤフー株式会社データ&サイエンスソリューション統括本部ソリューション本部でプログラマーをしております。趣味はカミさんの手料理です。
機械学習で用いられるアルゴリズムの一つにニューラルネットワークがあります。ニューラルネットワークは脳細胞の働きにヒントを得て考えられたものです。今回扱う多層ニューラルネットワークはニューラルネットワークの中間層と呼ばれる部分を多層化したものです。近年話題に上ることの多い Deep Learning ではこの多層ニューラルネットワークが利用されています。
多層ニューラルネットワークは用途に応じて異なるネットワークが利用されます。画像処理では畳込みニューラルネットワーク、自然言語処理では再帰型ニューラルネットワークなどです。
本稿ではまず Deep Learning の歴史を簡単に振り返り、次にシンプルかつ基本的で応用範囲が広い「順伝播型ニューラルネットワーク」を簡単に説明します。次に順伝播型ニューラルネットワークを実際に JavaScript で実装してみます。次にサンプルデータを使った性能評価の結果を掲載します。
本稿では数式を掲載しています。どのような数式に基いてコードが書かれているのかを説明したかったのが理由ですが、多少読みづらいかと思いますので、まずは数式を軽く読み飛ばしてプログラムをご覧いただき、このコードはどうしてこのような記述になっているのだろうと疑問に思われた時に再度数式を確認していただければと思います。
最初におわびですが、筆者は機械学習の専門家ではございません。詰めの甘い記述がかなりありますので、しっかりと理論を確認されたい方はぜひ参考文献をあたってみてください。
Deep Learning の歴史
Deep Learning という用語は通常、多層ニューラルネットワークを利用した機械学習の枠組みを意味するものとして使われています。ニューラルネットワークは 1940 年代に研究が開始されました。1958 年には F. Rosenblatt によって学習機能を持つパーセプトロンが発表されました。1969 年に M. Minsky らによってパーセプトロンが線形分離不可能な問題に対して有効でないことが指摘されるとニューラルネットワークのブームは下火となりました。その後、1986 年 D. E. Rumelhart らによって多層ニューラルネットワークの複雑な微分計算を容易にする誤差逆伝播法に関する論文が発表されたことにより、ニューラルネットワークは再び脚光を浴びることになります。しかしながらネットワークを多層にしたことにより発生する勾配消失問題が大きなネックになり、ブームは再度後退することとなりました。その後、2000 年代における G. E. Hinton による事前学習の研究によりニューラルネットワークは再度注目を集めることとなります。事前学習は、データをよく表す特徴を抽出し、それをもって重みの初期値を決定することにより、多層のネットワークでも勾配消失問題が起きにくくするものです。
2012 年に開催された大規模画像認識に関するコンペ ILSVRC(ImageNet Large Scale Visual Recognition Challenge)で優勝した A. Krizhevsky らのグループによる畳み込みニューラルネットワークは他をはるかに上回る成績を収め、これにより多層ニューラルネットワークの能力の高さが広く認識されるようになりました。
猫の画像が猫というカテゴリーに属すると判断するような画像のカテゴリー認識は長い間人間には容易でもコンピューターには難しい問題でしたが、Deep Learning の研究が進むにつれてこの難問は次第に解決されつつあります。
しかしながら、多層ニューラルネットワークもなぜ多層にすると精度が良くなるのかについては、まだ納得できる説明がなされていないようです。DeepLearning は今後もブームに流されない地道な研究が必要であると思われます。
順伝播型ニューラルネットワーク
順伝播型ニューラルネットワーク(Feed Forward Neural Network)は多層ニューラルネットワークの中でもシンプルで基本的なものです。本稿ではこの順伝播型ニューラルネットワークについて解説します。画像認識で用いられる畳み込みニューラルネットワーク(Convolutional Neural Network)はこの順伝播型ニューラルネットワークに畳み込み層、プーリング層、正規化層といった層を追加したものです。自然言語処理などで用いられる再帰型ニューラルネットワーク(Recurrent Neural Network)は系列データを処理する際、中間層の出力を次のデータの処理時に再度同じ中間層に入力させる経路を追加したもので、これにより前のデータによる影響を加味できるようにしたものです。順伝播型ニューラルネットワークはこういった多層ニューラルネットワークの基本になるものです。順伝播型ニューラルネットワークを習得することで畳み込みニューラルネットワークや再帰型ニューラルネットワークの実装もやりやすくなると思います。
ニューラルネットワーク
ニューラルネットワークは図 1 のように入力層、中間層、出力層で構成されます。それぞれの層にはユニットが複数存在します。ニューラルネットワークによる学習は、入力層にデータを与えて、出力層から出力された値を目標とする値に近くなるようにネットワークのパラメータを調整することです。最適なパラメータが与えられると、新しいデータを入力層に与えれば、そのデータを最もよく表現する出力値が出力層から出力されることになります。図 1 は出力層が 2 つありますが、問題の種類によって数は変化します。1 つの場合は線形回帰や 2 値分類問題、2 つ以上の場合は多値分類問題に対応します。
層の間をつなぐ線が層間結合です。順伝播型ニューラルネットワークでは、ある層のユニット全てとその前または後の層のユニット全てが結合されます。本稿では取り上げませんが、ドロップアウトというテクニックや、畳み込みニューラルネットワークなど、一部の層間結合がないケースがあります。
入力層のユニットにはそれぞれ 1 つの値が入力されます。問題の内容に応じて入力層のユニットは増減します。
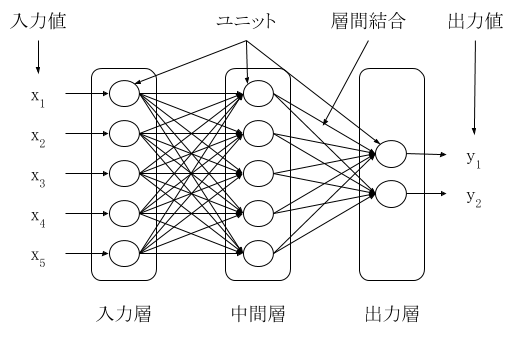
図 1: ニューラルネットワークの基本構成
多層ニューラルネットワーク
多層ニューラルネットワークは図 2 のように,中間層を複数つなげて多層にしたものです。図 2 では中間層のユニット数が等しくなっていますが、それぞれの層で異なっていても構いません。
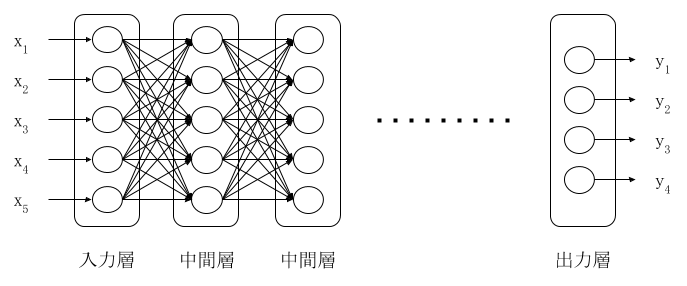
図 2: 多層ニューラルネットワーク
ニューラルネットワークの計算
ニューラルネットワークは全体として一つの関数と捉えることができます。入力層に入力された値がネットワーク内で計算され、出力層から値として取り出すイメージです。ここで図 3 のような層間のつながりを考えます。図 3 では連続した 2 つの層を p - 1 層と p 層と表します。u はユニットへの総入力、z はユニットからの出力、w は重みを表します。ここで b というバイアスを追加して p 層における j 番目のユニットの計算を表したのが式(1)、(2)です。w は結合ごとに定義されますが、b はユニットごとに定義される点に注意してください。
1,...,I は p - 1 層のユニットの番号で、1,...,J は p 層のユニットの番号とします。p - 1 や p は変数の右肩に付けました。wji は p - 1 層 における i 番目のユニットと p 層の j 番目のユニットを結んだ層間結合の重みを意味します。
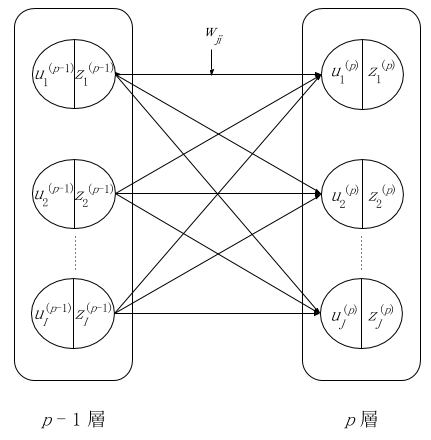
図 3: 層間における変数の関係
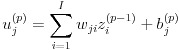 (1)
(1)
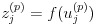 (2)
(2)
式(2)の f は活性化関数と呼ばれるもので、ユニットへの総入力にこの関数を適用してユニットの出力を得ます。得られた z は次の層への入力値として使われることになります。そのようにして式(1)および式(2)を出力層 P まで繰り返して計算します。
ここで、図 4 のようにバイアスを前の層の特別なユニット(バイアスユニットとします)との層間結合の重みとして考えると、u に関する計算式が式(3)のようにシンプルになります。図 4 では p 層のバイアスを p - 1 層の 0 番目のユニットとの結合の重み w として表現しました。本稿で実装するプログラムもこの形式で計算することにします。バイアスユニットからの出力値 z0p-1 は常に 0 となります。
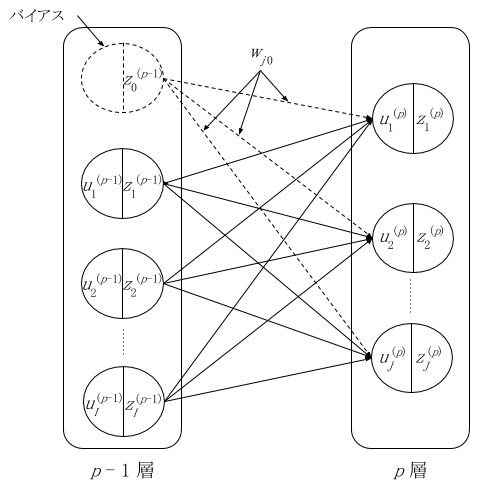
図 4: バイアスを前層のユニットとして構成した場合
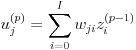 (3)
(3)
活性化関数
活性化関数はユニットへの入力値から出力値を計算する関数です。今回は中間層のユニットにおける活性化関数に式(4)の正規化線形関数(rectified linear function)を利用します。従来、ニューラルネットワークは式(5)のロジスティック関数(logistic function)や式(6)の双曲線正接関数が使われてきましたが、近年はその単純さと最終的な結果の良さにより、正規化線形関数が良く利用されます。本稿の実装も中間層には正規化線形関数を利用しています。
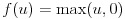 (4)
(4)
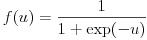 (5)
(5)
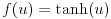 (6)
(6)
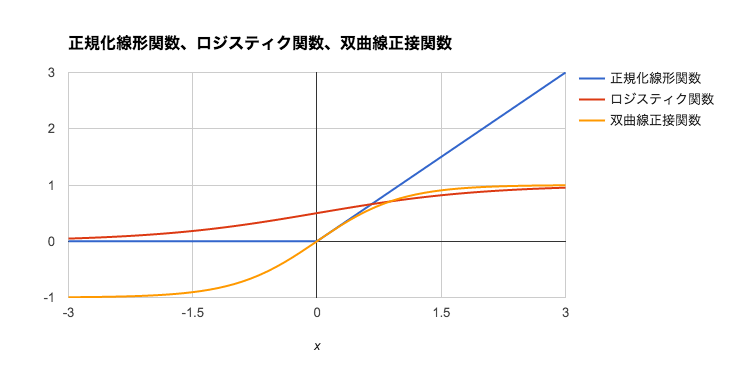
図 5: 正規化線形関数、ロジスティック関数、双曲線正接関数
出力層の活性化関数
出力層の活性化関数は一般に中間層の活性化関数とは違うものを用います。問題の性質により利用する関数は異なるのですが、本稿では多クラス分類を扱う順伝播ニューラルネットワークを解説することにします。多クラス分類では 式(7)のようなソフトマックス関数と呼ばれる関数が使用されます。ここで k は出力層における k 番目のユニット、P は P 番目の層、つまり出力層を表します。式(7)は出力層におけるユニット k の入力値の exp を出力層における全てのユニットの入力値の exp の和で割ることで k 番目のクラスが選択される「確率」を計算していると考えます。
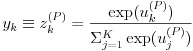 (7)
(7)
誤差関数
ニューラルネットワークではネットワークの目標値、つまり正解値と実際の出力値との間の関係を誤差関数という関数で表します。誤差関数は通常、損失関数と呼ばれることが多いですが、本稿では参考文献に倣い、誤差関数とさせていただきます。この関数を最小化するのが学習の目標になります。式(8)は多クラス分類における誤差関数です。難しい形をしていますが、後述の誤差逆伝播時の微分計算では単純な計算式に変形できるので便利です。この式の導出については参考文献をご参照下さい。ここで E は誤差関数、W は全ての重みとバイアスをまとめた行列、n はデータセットの番号、k は出力層のユニットの番号、dnk は n 番目のデータセットの k 番目のユニットが対応する出力の目標値、yk は出力層のユニット k の活性化関数、Xn はデータセット n のベクトルを表します。
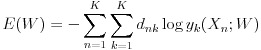 (8)
(8)
多クラス分類では学習時に入力値と目標値のセットをネットワークに入力します。目標値 d は例えばクラスが "犬"、"猫"、"羊" の 3 種類あって、出力層の 1 番目のユニットを犬、2 番目のユニットを猫、3 番目のユニットを羊に対応させた場合、犬のデータをセットするときは目標値として、(d1, d2, d3) = (1, 0, 0) を学習に利用します。
確率的勾配降下法
誤差関数の極小値を探索する方法はいくつか考えられますが、多層ニューラルネットワークでは勾配降下法が用いられることが多いようです。勾配降下法より一般的に収束が速いニュートン法は 2 階微分ですが、勾配降下法は 1 階微分ですので複雑なネットワークになることの多い多層ニューラルネットワークでは勾配降下法の方がよく使われます。この勾配降下法は全ての入力データによって計算された誤差関数の値に対し計算を行いますが、確率的勾配降下法は入力データをサンプリングします。こうすることでローカルな極小解にトラップされることを防いだり、計算時間を短縮できます。式(9)はバイアスを含んだ重みのパラメータ W で E を微分したもので、これを勾配と呼びます。式(10)はパラメータ W を勾配を使って修正しています、ε は学習係数と呼ばれるものです。この値を小さくすると勾配の更新が細かくなり、極小値が発見されやすくなりますが、反面収束のスピードが遅くなります。逆にこの値を大きくすると、学習スピードは速くなりますが、収束しない危険性が増してきます。学習係数の決定方法は AdaGrad などいくつかの方法が提案されていますが、本稿のプログラムでは学習前に決め打ちで指定することにします。式(11)は確率的勾配降下法、式(12)は確率的勾配降下法を用いたパラメータの更新を表します。n は分割した入力データ群の番号を意味します。確率的にデータを選択して学習することで、学習スピードが速くなり、学習がうまく進むケースが多くなります。理論的な詳細については参考文献をご参照下さい。
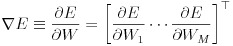 (9)
(9)
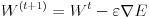 (10)
(10)
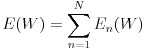 (11)
(11)
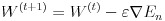 (12)
(12)
誤差逆伝播法
勾配降下法を適用する際、誤差関数の値 E を各層のユニット間結合に対する重み w とバイアス b (合わせて W としています)で微分します。この場合、出力層に近ければ微分はそれほど困難ではないのですが、出力層から離れて入力層に近くなる(深くなる)ほど微分計算は困難になります。仮に p 層の勾配を求めようとする場合、その層における出力は式(13)で表されますがネットワークが多層になるとこの入れ子の数は非常に多くなり、微分の連鎖法則を何度も適用する必要があります。従ってプログラミングも煩雑なものとなります。ここで X は入力値のベクトル、W は重みとバイアスを含んだ行列、Z は前の層の出力のベクトル、B はバイアスのベクトルとしています。
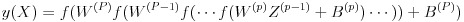 (13)
(13)
勾配計算の困難さを緩和するために、多層ニューラルネットワークにおける勾配の計算には誤差逆伝播法を用います。
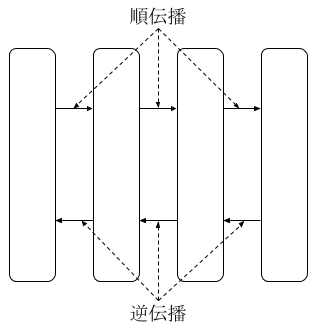
図 6: 順伝播と逆伝播
誤差逆伝播法の考え方は、出力層から入力層に向けて、前後の層の値を利用しながら勾配を計算していくものです。出力層の勾配をまず求めて、それをもとに一つ前の層の勾配を計算し、さらに前の勾配を計算するといった連鎖的な計算を行います。
n 番目のデータセットの誤差関数の値 En を層 p におけるパラメータ wji(p) で微分した式は式(3)により wji(p) が uj(p) にのみ影響をあたえることから連鎖法則により式(14)と展開できます。
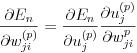 (14)
(14)
式(14)の右辺第 1 項は uj(p) が活性化関数を通して次の層の u1(p+1),...,uK(p+1) 全てに影響しており、かつ他には影響していないことにより、連鎖法則によって式(15)のように展開できます。
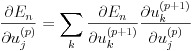 (15)
(15)
ここで式(16)のようにデルタを定義します。
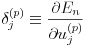 (16)
(16)
一方、uk(p+1) は、式 (17) のように変形できます。
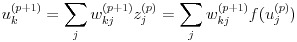 (17)
(17)
式(16)、(17)により、式(15)は式(18)のように表せます。
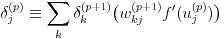 (18)
(18)
さらに式(14)の右辺第 2 項は式(19)の関係により、式(20)と表せます。
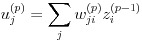 (19)
(19)
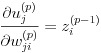 (20)
(20)
したがって最終的に誤差関数の出力 En の重み wji(p) による微分は式(21)で表すことができます。
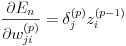 (21)
(21)
また、出力層のデルタについては式(22)で表せます。
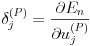 (22)
(22)
複数の学習データを確率的勾配降下法により学習する場合は、それぞれの En に対する微分を合計した式(23)を勾配としてパラメータの更新を行います。
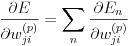 (23)
(23)
式(24)は誤差関数 En です。したがって、式(22)のデルタは式(25)のようになります。
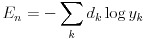 (24)
(24)
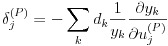 (25)
(25)
式 (25) の右辺の微分を式 (26) のように変形します。この部分の詳細な導出は参考文献をご参照下さい。
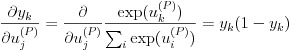 (26)
(26)
多クラス分類における出力層には、目標とするクラス k の目標値 dk のみが 1 で、他は 0 という性質があります。従って、出力の目標値 d の和は 1 に等しいことを利用すると、式(25)は式(27)で表すことができます。つまり、出力層のデルタはユニットの出力値と目標値との差にまで簡便化されることになります。後はこの値からスタートして誤差逆伝播法により任意の層のユニットにおけるデルタを計算すれば良くなります。
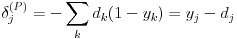 (27)
(27)
式(27)からスタートして 、式(18)のように p 層のデルタは p + 1 層のデルタ、p 層と p + 1 層との間の重み、p 層の活性化関数の 1 階微分関数の出力を掛け合わせたものを、p + 1 層のユニット分加算すれば誤差逆伝播の計算ができることになります。これにより、任意の層のデルタを求めることができますので、式(14)から任意の重みを更新できます。
正規化
入力データはそのままの値を使うより、正規化という処理を施す方が学習がうまく行くことが多いようです。本稿で扱うプログラムも、内部でデータの正規化処理を行っています。式(28)で平均値を計算し、式(29)で標準偏差を計算します。次に式(30)でデータの値から平均値を引いた値を標準偏差で割る形で正規化処理を行っています。
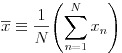 (28)
(28)
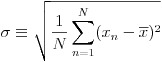 (29)
(29)
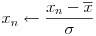 (30)
(30)
正規乱数
本稿では事前学習を使いません。従って、重みの初期値については何らかの値を与える必要があります。この場合、全ての重みに一定の値を与えるとうまく学習できません。従って乱数を与えることになりますが、この場合でも正規乱数を与える方が良い結果が出ます。なお、バイアスの初期値には通常 1 が使われます。
JavaScript には標準で正規乱数を生成するライブラリがありませんので、独自に実装する必要があります。今回は実装が簡単なボックス・ミュラー法を使うことにします。ボックス・ミュラー法による計算は式(31)または(32)で与えられます。x と y は Math.rand() で生成する乱数です。
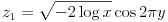 (31)
(31)
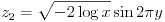 (32)
(32)
実装の準備
JavaScript のコーディングと実行する環境があれば何でも OK です。筆者は Mac の vim でコーディングをして Node.js と Chrome のそれぞれで動作確認をしました。Windows のメモ帳と(最新の)IE を使ってもおそらく大丈夫ではないかと思いますが確認をしていません。ごめんなさい。
ちなみに筆者は Windows でコーディングする際、良くメモ帳を使います。
実装
それでは実際のコードを見ながら実装を確認していきます。なお、今回のコードは行列やベクトルを使っていませんが、実際の実装は行列やベクトル計算のライブラリを使う方がすっきりとした実装になります。行列やベクトルを使った実装の方法については参考文献をご参照下さい。
ユーティリティー
正規乱数やデータの正規化のための関数を集めたクラスを作りました。なお、DNN は Deep Neural Network の略です。以降同様とします。
正規乱数
式(31)を使って正規乱数を計算している部分です。前半はオブジェクトの定義の部分です。
// ユーティリティー関数
var DNNUtil = function() {
};
// ユーティリティー関数定義
DNNUtil.prototype = {
// 正規乱数
rnorm: function(mean, sd) {
var x = Math.random();
var y = Math.random();
var ret = mean + sd * Math.sqrt(-2 * Math.log(x)) * Math.cos(2 * Math.PI * y);
return ret;
},配列からランダムに取得
配列から指定された個数ランダムに抜き出して配列として返します。確率的勾配降下など、データをランダムにサンプリングする用途で使っています。
randomChoice: function (ary, count) {
// 配列のサイズが指定サイズ以下ならそのまま返します。
if (ary.length <= count) {
return ary;
}
// 新しい配列
var newAry = [];
// 使用済みインデックス
var used = {};
// 新しい配列が規定の数になるまでループします。
while (true) {
// 乱数
var r = Math.floor(Math.random() * ary.length);
// 既に使われている場合はスキップ
if ((r in used)) {
continue;
}
newAry.push(ary[r]);
// 規定の数になったら break
if (newAry.length == count) {
break;
}
used[r] = 1;
}
return newAry;
},平均と標準偏差
連想配列の配列から連想配列中の data の平均と標準偏差を取得します。式(28)、(29)に対応します。
getMeanAndSD: function(dataSet) {
// 合計の計算
var sum = [];
for (var i = 0; i < dataSet.length; i++) {
var items = dataSet[i]['data'];
for (var j = 0; j < items.length; j++) {
if (sum[j] === undefined) {
sum[j] = 0;
}
sum[j] += items[j];
}
}
// 平均
var means = [];
for (var k = 0; k < sum.length; k++) {
means[k] = sum[k] / dataSet.length;
}
// 差の2乗の合計
var squaredSum = [];
for (var l = 0; l < dataSet.length; l++) {
var items2 = dataSet[l]['data'];
for (var m = 0; m < items2.length; m++) {
if (squaredSum[m] === undefined) {
squaredSum[m] = 0;
}
squaredSum[m] += Math.pow((items2[m] - means[m]), 2);
}
}
// 標準偏差
var sds = [];
for (var p = 0; p < dataSet.length; p++) {
var items3 = dataSet[p]['data'];
for (var q = 0; q < items3.length; q++) {
var sd = Math.sqrt(squaredSum[q] / dataSet.length);
sds[q] = sd;
}
}
return {means: means, sds: sds};
},平均と標準偏差で正規化
配列を指定された平均と標準偏差で正規化します。式(30)に対応します。
normalize: function(dataAry, mean, sd) {
var newAry = [];
for (var i = 0; i < dataAry.length; i++) {
newAry.push((dataAry[i] - mean[i]) / sd[i]);
}
return newAry;
}
};ユニットタイプ
ユニットタイプを定義します。このタイプをユニットオブジェクトにセットすることで、ユニットに応じた処理を行うようにします。ここではバイアスユニットという特別なユニットも定義しました。バイアスユニットは式(1)のバイアス b に対応します。
INPUT は入力層のユニット、HIDDEN は中間層のユニット、BIAS はバイアスユニット、OUTPUT は出力層のユニットです。
var UnitType = {
INPUT: 0,
HIDDEN: 1,
BIAS: 2,
OUTPUT: 3
};ユニットクラスのコンストラクタ部分
厳密にはコンストラクタではないと思いますが、コンストラクタのようなものとさせてください。筆者の JavaScript に関する知識はスライムレベルです。
// ユニットクラス
var Unit = function(unitType) {
// ユニットタイプ
this.unitType = unitType;
// ユニット自体に左右の結合オブジェクトへの参照を持たせることで lookup を容易にしています。
// 結合オブジェクト(左側)
this.leftConnections = [];
// 結合オブジェクト(右側)
this.rightConnections = [];
// 入力値 全結合層の場合は前の層の全ユニットからの出力の合計とバイアスの合計です。
// 今回はバイアスユニットの出力と重みも加算されます。
this.inputValue = 0;
// 出力値(バイアスの出力は1固定になります。)
this.outputValue = 0;
if (unitType === UnitType.BIAS) {
this.outputValue = 1;
}
// デルタ
// 誤差逆伝播法で重要な要素になります。ユニットオブジェクトに持たせます。
this.delta = 0;
};ユニットクラスの定義部分
基本的に setter/getter です。左側結合は中間層と出力層にしかないので他のユニットタイプの場合は例外を出すといったようなチェックをしています。
// ユニットクラス定義
Unit.prototype = {
// ユニットタイプの取得
getUnitType: function(unitType) {
return this.unitType;
},
// 結合オブジェクト(左側)の配列を設定
setLeftConnections: function(connections) {
// 中間層と出力層のみ
if (this.unitType !== UnitType.HIDDEN &&
this.unitType !== UnitType.OUTPUT) {
throw new Error('Invalid unit type');
}
this.leftConnections = connections;
},
// 結合オブジェクト(右側)の配列を設定
setRightConnections: function(connections) {
// 入力層と中間層とバイアスのみ
if (this.unitType !== UnitType.INPUT &&
this.unitType !== UnitType.HIDDEN &&
this.unitType !== UnitType.BIAS) {
throw new Error('Invalid unit type');
}
this.rightConnections = connections;
},
// 結合オブジェクト(左側)の配列を取得
getLeftConnections: function() {
// 中間層と出力層のみ
if (this.unitType !== UnitType.HIDDEN &&
this.unitType !== UnitType.OUTPUT) {
throw new Error('Invalid unit type');
}
return this.leftConnections;
},
// 結合オブジェクト(右側)の配列を取得
getRightConnections: function() {
// 入力層と中間層とバイアスのみ
if (this.unitType !== UnitType.INPUT &&
this.unitType !== UnitType.HIDDEN &&
this.unitType !== UnitType.BIAS) {
throw new Error('Invalid unit type');
}
return this.rightConnections;
},
// 入力値を設定
setInput: function(value) {
// 入力層と中間層と出力層のみ
if (this.unitType !== UnitType.INPUT &&
this.unitType !== UnitType.HIDDEN &&
this.unitType !== UnitType.OUTPUT) {
throw new Error('Invalid unit type');
}
this.inputValue = value;
},
// 入力値を取得
getInput: function() {
// 入力層と中間層と出力層のみ
if (this.unitType !== UnitType.INPUT &&
this.unitType !== UnitType.HIDDEN &&
this.unitType !== UnitType.OUTPUT) {
throw new Error('Invalid unit type');
}
return this.inputValue;
},
// 出力値を設定
setOutput: function(value) {
this.outputValue = value;
},
// 出力値を取得
getOutput: function() {
return this.outputValue;
},
// デルタを設定
setDelta: function(delta) {
// 中間層と出力層のみ
if (this.unitType !== UnitType.HIDDEN &&
this.unitType !== UnitType.OUTPUT) {
throw new Error('Invalid unit type');
}
this.delta = delta;
},
// デルタを取得
getDelta: function() {
// 中間層と出力層のみ
if (this.unitType !== UnitType.HIDDEN &&
this.unitType !== UnitType.OUTPUT) {
throw new Error('Invalid unit type');
}
return this.delta;
}
};コネクションクラスのコンストラクタ部分
層間結合を保持するオブジェクトです。内部には結合の両側のユニットオブジェクト、重み、重みの差分を保持しています。誤差逆伝播を計算している間、重みの差分はこちらに保存しておき、誤差逆伝播の終わりにまとめてして this.weight に加算(減算)します。誤差逆伝播の計算中は更新前の値が必要になるためです。
var Connection = function() {
// ユニット(左側)
this.leftUnit = {};
// ユニット(右側)
this.rightUnit = {};
// 重み
this.weight = 1;
// 重みの差分(一時保存用)
this.weightDiff = 0;
};コネクションクラスの定義部分
層間結合のオブジェクトは基本的に setter/getter のみです。
// コネクションクラス定義
Connection.prototype = {
// ユニット(左側)の設定
setLeftUnit: function(unit) {
this.leftUnit = unit;
},
// ユニット(右側)の設定
setRightUnit: function(unit) {
this.rightUnit = unit;
},
// ユニット(左側)の取得
getLeftUnit: function() {
return this.leftUnit;
},
// ユニット(右側)の取得
getRightUnit: function() {
return this.rightUnit;
},
// 重みの設定
setWeight: function(weight) {
this.weight = weight;
},
// 重みの取得
getWeight: function() {
return this.weight;
},
// 重みの差分の設定
setWeightDiff: function(diff) {
this.weightDiff = diff;
},
// 重みの差分の取得
getWeightDiff: function() {
return this.weightDiff;
}
};多層ニューラルネットワークのメイン部分のコンストラクタ
メイン部分です。ちょっと長いですが重要な処理をしています。分割して記載します。最初は変数部分です。
// パラメータは下記のような形式で渡します。
// {numOfUnits:[], weights:[[],...], means:[], sds:[]}
// なお、weights、means、sds は任意です。
var DNN = function(param) {
// パラメータチェック
if (param === null || param === undefined) {
throw new Error("Null parameter.");
}
if ('numOfUnits' in param === false) {
throw new Error("numOfUnits must be specified.");
}
if (param['numOfUnits'].length <= 2) {
throw new Error("At least 1 hidden units must be specified.");
}
// デフォルトの重み
this.DEFAULT_WEIGHT = 0;
// ユニット数
this.numOfUnits = param['numOfUnits'];
// 学習係数(Default)
this.learningCoefficient = 0.01;
// ミニバッチサイズ
this.miniBatchSize = 10;
// 接続オブジェクト
this.connections = {};
// ユニットオブジェクト
this.units = {};
// 入力値の平均
this.inputMeans = [];
if ('means' in param) {
this.inputMeans = param['means'];
}
// 入力値の標準偏差
this.inputSDs = [];
if ('sds' in param) {
this.inputSDs = param['sds'];
}次に各層を初期化します。初期化は層ごとにその層のユニットオブジェクトを生成して配列に追加する形で行います。また、出力層の他の層は先頭にバイアスユニットを生成してセットします。
////// 各種初期化プロセス
// 全ての層をまとめたもの
var layersArray = [];
// 入力層の初期化(バイアスユニットを先頭に持ってきます)
var inputUnitArray = [];
inputUnitArray.push(new Unit(UnitType.BIAS)); // BIAS
for (var i = 0; i < this.numOfUnits[0]; i++) {
inputUnitArray.push(new Unit(UnitType.INPUT));
}
layersArray.push(inputUnitArray);
// 中間層の初期化(バイアスユニットを先頭に持ってきます)
for (var j = 1; j < this.numOfUnits.length - 1; j++) {
var hiddenUnitArray = [];
hiddenUnitArray.push(new Unit(UnitType.BIAS)); // BIAS
for (var k = 0; k < this.numOfUnits[j]; k++) {
hiddenUnitArray.push(new Unit(UnitType.HIDDEN));
}
layersArray.push(hiddenUnitArray);
}
// 出力層の初期化
var outputUnitArray = [];
for (var l = 0; l < this.numOfUnits[this.numOfUnits.length - 1]; l++) {
outputUnitArray.push(new Unit(UnitType.OUTPUT));
}
layersArray.push(outputUnitArray);初期化したコネクションオブジェクトに左右のユニットを加えていきます。同時にコネクションの重みを設定しますが、バイアスユニットではないユニットからのコネクションの重みは平均 0 、標準偏差 1 の乱数で初期化します。
// ユニットオブジェクト
this.units = layersArray;
// Util
var dnnUtil = new DNNUtil();
// コネクションの生成
var allConnectionArray = [];
// 層の数 - 1 のコネクション「層」が必要
for (var m = 0; m < this.numOfUnits.length - 1; m++) {
// 現在のコネクション層
var connectionArray = [];
// 現在のコネクション層の左側のユニットをループ
for (var n = 0; n < this.units[m].length; n++) {
// 左のユニット毎にそのユニットの右に出ているコネクション
var connArray = [];
// 左ユニット
var leftUnit = this.units[m][n];
// 右隣のユニットをループ
for (var p = 0; p < this.units[m + 1].length; p++) {
var rightUnit = this.units[m + 1][p];
// 右隣のバイアスユニットは除く
if (rightUnit.getUnitType() !== UnitType.BIAS) {
var conn = new Connection();
// 現在のコネクション層の右側のユニットをセット
conn.setRightUnit(rightUnit);
// 現在のコネクション層の左側のユニットをセット
conn.setLeftUnit(leftUnit);
// 重みの設定
if (leftUnit.getUnitType() === UnitType.BIAS) {
// 左のユニットがバイアスユニットの場合
conn.setWeight(this.DEFAULT_WEIGHT);
} else {
// 左のユニットがバイアスユニットでない場合
conn.setWeight(this.DEFAULT_WEIGHT + dnnUtil.rnorm(0, 1));
}
connArray.push(conn);
// 右ユニットの左側コネクションに追加
var connTmpArray = rightUnit.getLeftConnections();
connTmpArray.push(conn);
rightUnit.setLeftConnections(connTmpArray);
}
}
// 現在のコネクション層に追加
connectionArray.push(connArray);
// 左ユニットの右側結合にセット
leftUnit.setRightConnections(connArray);
}
// 全てのコネクションに追加
allConnectionArray.push(connectionArray);
}既存のモデルをセットする場合等、重みが指定されている場合、重みを層間結合オブジェクト(コネクションオブジェクト)にセットします。
// 全てのコネクション
this.connections = allConnectionArray;
// weightsが指定されている場合
if ('weights' in param) {
// 重みのみの配列から重みを対応するconnectionにそれぞれ設定する
for (var s = 0; s < this.connections.length; s++) {
for (var t = 0; t < this.connections[s].length; t++) {
for (var u = 0; u < this.connections[s][t].length; u++) {
this.connections[s][t][u].setWeight(param['weights'][s][t][u]);
}
}
}
}
};多層ニューラルネットワークメインクラスの定義部分(train, test, predict を除く)
学習、テスト、判定といった大きな処理を除いた部分です。学習係数の設定ができるようにします。getModel で取得したモデルオブジェクトを保存しておくことで、学習したモデルを何度でも使い回すことができます。
// DNNメインクラス定義
DNN.prototype = {
// 学習係数の設定
setLearningCoefficient: function(coefficient) {
this.learningCoefficient = coefficient;
},
// ミニバッチサイズの設定
setMiniBatchSize: function(size) {
this.miniBatchSize = size;
},
/**
* モデルの取得
* 各層のユニット数と重みを返す
* {
* numOfUnits:[入力層のユニット数,中間層1のユニット数,...,出力層のユニット数],
* weights:[[重み,...],[..],...],
* means:[入力値1の平均,入力値2の平均,...],
* sds:[入力値1の標準偏差,入力値2の標準偏差,...],
* }
*/
getModel: function() {
var weights = [];
for (var i = 0; i < this.connections.length; i++) {
var weightsSub = [];
for (var j = 0; j < this.connections[i].length; j++) {
var weightsSubSub = [];
for (var k = 0; k < this.connections[i][j].length; k++) {
weightsSubSub.push(this.connections[i][j][k].getWeight());
}
weightsSub.push(weightsSubSub);
}
weights.push(weightsSub);
}
return {numOfUnits:this.numOfUnits,
weights:weights,
means:this.inputMeans,
sds:this.inputSDs};
},学習
学習処理です。確率的勾配降下、誤差逆伝播を行う重要な関数です。最初にデータセットを式(28)、(29)、(30)に基づいて正規化します。次にミニバッチと呼ばれるランダムに選択したデータの 1 単位ごとに処理する方法で学習します。出力層のデルタは式(27)に基いて出力値と目標値の差で計算しています。また、式(18)に基づいて、中間層のユニットのデルタを計算しています。なお、正規化線形関数の 1 階微分はユニットの入力が 0 未満の場合は 0 、0 以上の場合は 1 になります。次に式(21)で重みごとの勾配を計算し、式(12)に基いて重みの更新を行っています。
/**
* 学習
* @param data [{data:[a_1,a_2,...,a_n], expected:c}],[...],...
* @return
*/
train: function(dataSet) {
// データセットの平均と標準偏差を取得
var dnnUtil = new DNNUtil();
var msd = dnnUtil.getMeanAndSD(dataSet);
this.inputMeans = msd['means'];
this.inputSDs = msd['sds'];
// ミニバッチ用データ選択
var data = dnnUtil.randomChoice(dataSet, this.miniBatchSize);
// {クラス,データ}のペアを繰り返し処理
for (var n = 0; n < data.length; n++) {
// 判定処理を実行して各層の入力、出力を確定させる
this.predict(data[n]['data']);
// 誤差逆伝播(まず重みの差分を計算、あとでまとめて更新する)
// 出力層から順に
// 入力層は除く
for (var k = this.numOfUnits.length - 1; k > 0; k--) {
for (var l = 0; l < this.units[k].length; l++) {
// ユニット
var unit = this.units[k][l];
// デルタ
var delta = 0;
// 出力層か中間層のユニットの場合(バイアスは除く)
if (unit.getUnitType() === UnitType.OUTPUT || unit.getUnitType() === UnitType.HIDDEN) {
// 出力層のユニットの場合
if (unit.getUnitType() === UnitType.OUTPUT) {
// 出力層のデルタは y - d
delta = unit.getOutput();
// 期待されるクラスの場合は-1する(出力層のデルタはy - dなので)
if (data[n]['expected'] == l) {
delta -= 1;
}
// 中間層のユニット(バイアスは除外)
} else {
// 入力値
var inputValue = unit.getInput();
// 上位層のユニットを右側結合を通じてループ
var rightConns = unit.getRightConnections();
for (var m = 0; m < rightConns.length; m++) {
// デルタ * 重み * 正規化線形関数の1階微分
delta += rightConns[m].getRightUnit().getDelta() *
rightConns[m].getWeight() *
((inputValue < 0) ? 0 : 1);
}
}
// デルタをセット
unit.setDelta(delta);
// 重みの差分を前回の逆伝播の結果に追加(左側結合の全て)
var conns = unit.getLeftConnections();
for (var p = 0; p < conns.length; p++) {
var diff = conns[p].getWeightDiff();
// デルタ * 左側ユニットの出力
diff += delta * conns[p].getLeftUnit().getOutput();
conns[p].setWeightDiff(diff);
}
}
}
}
// 誤差逆伝播(重みの更新)
// connectionに重みの差分がセットされているのでそれらを順次適用する
for (var q = 0; q < this.connections.length; q++) {
for (var r = 0; r < this.connections[q].length; r++) {
for (var s = 0; s < this.connections[q][r].length; s++) {
var conn = this.connections[q][r][s];
var weight = conn.getWeight();
weight -= this.learningCoefficient * conn.getWeightDiff();
// 新しい重みをセット
conn.setWeight(weight);
// 重みの差分をクリア
conn.setWeightDiff(0);
}
}
}
}
},テスト
誤差関数の値を計算するための関数です。学習は誤差関数の値の計算→誤差逆伝播→誤差関数の値の計算→誤差逆伝播、…という風に繰り返して行います。
/**
* テスト
* @param data [{data:[a_1,a_2,...,a_n], expected:c}],[...],...
* @return 誤差関数の値
*/
test: function(dataSet) {
// 誤差
var e = 0;
// ミニバッチ用データ選択
var dnnUtil = new DNNUtil();
var data = dnnUtil.randomChoice(dataSet, this.miniBatchSize);
// {クラス,データ}のペアを繰り返し処理
for (var n = 0; n < data.length; n++) {
// 判定処理を実行して各層の入力、出力を確定させる
this.predict(data[n]['data']);
// 出力層
var outputUnits = this.units[this.numOfUnits.length - 1];
// 出力層の出力の合計
var sum = 0;
// 誤差関数の計算
for (var i = 0; i < outputUnits.length; i++) {
// クラスが一致した場合のみ出力の対数値を加算(クラスが一致しない場合は0をかけるので)
if (data[n]['expected'] == i) {
sum += Math.log(outputUnits[i].getOutput());
}
}
// 符号を反転して加算
e += -1 * sum;
}
// eの平均値を返す
var avg_e = e / data.length;
return avg_e;
},判定
DNN オブジェクトが学習済みの状態であるか、外部からモデルを設定された状態で判定を行います。モデルが設定されているとは、ネットワークのパラメータ、重みとバイアスに学習済みの値がセットされている状態を指します。
出力層の計算時には式(7)のソフトマックス関数を使っています。ソフトマックス関数の値が最も大きい k を判定結果とします。受け取り側はこの k に対応するクラスを最終的な判定結果とすれば良いことになります。
/**
* 判定
* @param data [a_1,a_2,...,a_n]
* @return best: 最も値の高かった出力層のユニットのインデックス
* result: 最も値の高かった出力層のユニットの値
*/
predict: function(dataSet) {
// ソフトマックス関数の計算用
var denom = 0;
var denomArray = [];
// データセットを正規化する
var dnnUtil = new DNNUtil();
var data = dnnUtil.normalize(dataSet, this.inputMeans, this.inputSDs);
// バイアスを除く入力層のユニット全部
// 現在の層のユニット全部
var g = 0;
for (var h = 0; h < this.units[0].length; h++) {
if (this.units[0][h].getUnitType() != UnitType.BIAS) {
// 入力層は入力値=出力値
this.units[0][h].setInput(data[g]);
this.units[0][h].setOutput(data[g]);
g++;
}
}
// 入力層以降から繰り返し
for (var i = 1; i < this.units.length; i++) {
// 現在の層のユニット全部
for (var j = 0; j < this.units[i].length; j++) {
var unit = this.units[i][j];
// 中間層と出力層の場合(バイアスの出力は常に1なので処理しない)
if (unit.getUnitType() === UnitType.HIDDEN ||
unit.getUnitType() === UnitType.OUTPUT) {
// 左側ユニットの出力*重みの合計
var sum = 0;
// 左結合
var connArray = unit.getLeftConnections();
for (var k = 0; k < connArray.length; k++) {
var conn = connArray[k];
// 左側ユニットの出力 * 左側結合の重みを加算
sum += conn.getLeftUnit().getOutput() * conn.getWeight();
}
unit.setInput(sum);
// 出力層の場合はソフトマックス関数計算用変数をセット
if (unit.getUnitType() === UnitType.OUTPUT) {
var ex = Math.exp(unit.getInput());
denom += ex;
denomArray.push(ex);
// 中間層の場合は正規化線形関数
} else {
if (unit.getInput() < 0) {
unit.setOutput(0);
} else {
unit.setOutput(unit.getInput());
}
}
}
}
}
// ソフトマックス関数計算用変数からOUTPUTユニットの最終結果を計算
var result = [];
var outputUnits = this.units[this.numOfUnits.length - 1];
for (var p = 0; p < denomArray.length; p++) {
var res = denomArray[p] / denom;
result.push(res);
// outputに出力値をセットする。学習時の誤差関数に出力が必要になる
outputUnits[p].setOutput(res);
}
// 最も確率の高い結果を調べる
var best = -1;
var idx = -1;
for (var q = 0; q < result.length; q++) {
if (best < result[q]) {
best = result[q];
idx = q;
}
}
return {best:idx, result:result};
}
}; Node.js 用
Node.js で処理する場合は下記を追記しておきます。
module.exports.DNN = DNN;評価
では早速評価してみます。Deep Learning では MNIST の手書き文字データを使って評価をする例が多いですが、今回のネットワークは畳み込みニューラルネットワークではないことと、著者の力不足で準備に時間が掛けられなかったので、機械学習全般の評価でよく使われる Fisher's Iris Dataset を使ってみます。
評価に使ったプログラムを下記に掲載しておきます。Node.js で処理することを想定しています。HTML に組み込む場合でも参考になると思います。
// パラメータのチェック
if (process.argv.length !== 3) {
console.log("Usage: node cross_validation.js <training data file>");
process.exit();
}
// ファイルシステムオブジェクト
var fs = require('fs');
var dataFile = process.argv[2];
// DNN.js の読み込み
var DNN = require('./DNN.js');
// 下記のネットワーク構成とします。
// 入力層: 4 ユニット
// 中間層: 4, 4 ユニット
// 出力層: 3 ユニット
var dnn = new DNN.DNN({numOfUnits:[4, 4, 4, 3]});
// 学習係数の設定
dnn.setLearningCoefficient(0.001);
// 学習データを読み込みます。
var data = fs.readFileSync(dataFile, 'utf-8');
// 改行で split します。データセットの取得先によって変わるかも。
var lines = data.split("\r\n");
// 10-fold cross validation を行います。
// 1 分割あたりのデータ数を計算
var size = Math.floor(lines.length / 10);
// 全てのデータセット
var allDataSets = [];
var i = 0;
// 精度計算用
var accuracySum = 0;
// ループ
while (1) {
// データセット
var dataSets = [];
// 1 分割あたりのデータ数までを dataSets にセットします。
for (var j = 0; j < size; j++) {
if (i > lines.length - 1) {
break;
}
var ary = lines[i].split("\t");
dataSets.push(ary);
i++;
}
// 全データセットに配列として追加します。
allDataSets.push(dataSets);
// 10 データセットになったら break
if (allDataSets.length == 10) {
break;
}
}
// 全データセット分ループ
for (var i = 0; i < allDataSets.length; i++) {
// 学習データとテストデータ
var trainData = [];
var testData = [];
// 再度全データセット分ループ
for (var j = 0; j < allDataSets.length; j++) {
// データセットをループ
for (var k = 0; k < allDataSets[j].length; k++) {
// テストデータを保存
if (i == j) {
testData.push(allDataSets[j][k]);
// 学習データを保存
} else {
trainData.push(allDataSets[j][k]);
}
}
}
// 誤差関数の出力が規定の値未満になるまで最大 10000 回ループします。
for (var l = 0; l < 10000; l++) {
// DNN.js に渡すデータ
var inputData = [];
for (var m = 0; m < trainData.length; m++) {
// ラベル部分を除外したもの
var dataPart = [];
for (var n = 1; n < trainData[m].length; n++) {
dataPart.push(Number(trainData[m][n]));
}
// DNN.js に渡すデータに追加
inputData.push({expected:Number(trainData[m][0]), data:dataPart});
}
// 学習処理
dnn.train(inputData);
// 1 学習後のネットワークに対して入力データによる誤差関数の値を取得
var result = dnn.test(inputData);
// 誤差関数の値が 0.01 未満であれば break
if (result < 0.01) {
break;
}
}
// 正解数
var corrects = 0;
// テストデータをループしてテスト
for (var o = 0; o < testData.length; o++) {
// ラベル以外の部分
var dataPart = [];
for (var p = 1; p < testData[o].length; p++) {
dataPart.push(Number(testData[o][p]));
}
// 判定
var result = dnn.predict(dataPart);
// best には最も値の高かったラベルが入っています。
if (result['best'] == Number(testData[o][0])) {
corrects++;
}
}
// 1 回のループ(学習と判定)における精度の平均値を加算
accuracySum += 100 * corrects / testData.length;
}
// 全ループによる精度の平均値を出力
console.log("accuracy: " + (accuracySum / allDataSets.length) + "%"); SVM(Support Vector Machine)との比較もしてみます。SVM は libsvm を利用しました。
libsvm
libsvm に付属している grid.py で c と g の最適値を探索して処理しました。97.3333% です。
$ ../../github/libsvm/svm-train -c 8192 -g 3.0517578125e-05 -v 10 -q train_data_fisher_libsvm.txt
Cross Validation Accuracy = 97.3333%最適化前だと下記のようになりました。82.6667% です。
$ ../../github/libsvm/svm-train -v 10 -q train_data_fisher_libsvm.txt
Cross Validation Accuracy = 82.6667%DNN.js
$ node cross_validation.js train_data_fisher.txt
accuracy: 97.33333333333333%libsvm が約 97.33% で多層ニューラルネットワークも約 97.33% でした。
今回のプログラムでは重みの初期値を正規乱数で設定しており、誤差関数の値が一定値以下で学習を打ち切っているいるため、処理する度に評価が変わります。念のため、10 回処理してみたところ平均は 96.00% でした。
| 回数 | Accuracy |
|---|---|
| 1 | 94.67% |
| 2 | 96.00% |
| 3 | 97.33% |
| 4 | 93.99% |
| 5 | 95.33% |
| 6 | 96.66% |
| 7 | 96.00% |
| 8 | 97.33% |
| 9 | 95.33% |
| 10 | 97.33% |
| 平均 | 96.00% |
結果
SVM との比較結果を掲載します。Fisher's Iris Dataset の学習に今回の多層ニューラルネットワークを使うと、最適なパラメータを使用した SVM と同等の性能が出たことがわかります。
| アルゴリズム | Accuracy |
|---|---|
| SVM(libsvm)※パラメータ最適化なし | 82.67% |
| SVM(libsvm)※パラメータ最適化あり | 97.33% |
| 多層ニューラルネットワーク ※平均 | 96.00% |
| 多層ニューラルネットワーク ※ベスト | 97.33% |
画像認識など、もっと特徴量が多くて複雑な問題だと差が出てくるかもしれません。
事前学習
事前学習は、データをよく表す特徴を抽出し、それをもって重みの初期値を決定することにより、多層のネットワークでも勾配消失問題が起きにくくするものです。事前学習の研究が Deep Learning にブレークスルーをもたらしましたが、近年では事前学習を用いないでうまく学習する方法も提案されています。
今回の JavaScript では事前学習を実装していません。代わりに正規化線形関数を使ったり、データを正規化したり、重みの初期値を正規乱数にしたりといった細かいテクニックを用いています。ただ、より複雑なデータでより複雑なネットワークを構成して学習を行う場合は事前学習の実装を検討した方が良いと思います。
おわりに
長々とお付き合いいただきありがとうございました。Deep Learning を JavaScript で実装してみた今回の Tech Blog はいかがでしたでしょうか。検証用ネットワークの中間層やユニットの数が少な過ぎて全然 Deep じゃない、とのお叱りはごもっともです。申し訳ございません。コードが読みづらいとのお叱りもごもっともです。申し訳ございません。次はより良いものになるよう努力します。
なお、今回紹介した JavaScript プログラムはユニット数や中間層の数に制限は設けておりませんのでメモリの許す限り複雑なネットワークを構成することも可能です。みなさんもぜひ挑戦してみてください。
終わりになりましたが、皆様が良いお年を迎えられるよう心からお祈りしております。それでは。
参考文献
- 岡谷貴之. (2015). 機械学習プロフェッショナルシリーズ 深層学習. 講談社.
- 本稿の執筆で最も参考にさせていただきました。ありがとうございました。
- 本稿の執筆で最も参考にさせていただきました。ありがとうございました。
鈴木大慈. (2015). 機械学習プロフェッショナルシリーズ 確率的最適化. 講談社.
Asuncion, A., & Newman, D. (2007). UCI machine learning repository.
- Fisher's Iris Dataset があります。
Hochreiter, S. (1998). The vanishing gradient problem during learning recurrent neural nets and problem solutions. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 6(02), 107-116.
- Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems (pp. 1097-1105).
Nair, V., & Hinton, G. E. (2010). Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10) (pp. 807-814).
- Rumelhart, D. E. (1986). David E. Rumelhart, Geoffrey E. Hinton, and Ronald J. Williams. Nature, 323, 533-536.
こちらの記事のご感想を聞かせください。
- 学びがある
- わかりやすい
- 新しい視点
ご感想ありがとうございました



